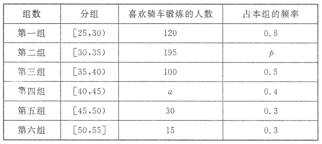
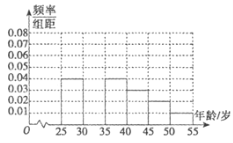
题目内容
【题目】已知函数![]()
(1)若![]() ,求函数
,求函数![]() 的表达式;
的表达式;
(2)在(1)的条件下,设函数![]() ,若
,若![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)是否存在![]() 使得函数
使得函数![]() 在
在![]() 上的最大值是4?若存在,求出
上的最大值是4?若存在,求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)存在,
;(3)存在,![]() 或
或![]() 。
。
【解析】
试题分析:(1)![]() ,所以
,所以![]() ,此时函数
,此时函数![]() ;(2)在(1)的条件下
;(2)在(1)的条件下![]() ,函数
,函数![]() 为二次函数,对称轴为
为二次函数,对称轴为![]() ,若函数
,若函数![]() 在区间
在区间![]() 上是单调函数,则应满足
上是单调函数,则应满足![]() 或
或![]() ,解得:
,解得:![]() 或
或![]() ;(3)函数
;(3)函数![]() 的对称轴方程为
的对称轴方程为![]() ,分
,分![]() 和
和![]() 两种情况进行讨论,当
两种情况进行讨论,当![]() 时,开口向上,对称轴
时,开口向上,对称轴![]() ,此时函数
,此时函数![]() 在区间
在区间![]() 上的最大值应在
上的最大值应在![]() 时取得,即
时取得,即![]() ,解得:
,解得:![]() 与
与![]() 矛盾,当
矛盾,当![]() 时,开口向下,此时函数最大值应在
时,开口向下,此时函数最大值应在![]() 或
或![]() 或
或![]() 处取得,经验证,在
处取得,经验证,在![]() 及
及![]() 处取得最大值均不符合题意,若在
处取得最大值均不符合题意,若在![]() 处取得最大值,则
处取得最大值,则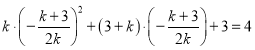 ,整理得
,整理得![]() ,所以
,所以![]() 或
或![]() ,此时对称轴分别为
,此时对称轴分别为![]() 和
和![]() ,均符合题意。
,均符合题意。
试题解析:(1)∵![]() 解得
解得![]()
∴![]()
(2)由(1)可得 ![]()
![]()
其对称轴方程为![]()
若![]() 在
在![]() 上为增函数,则
上为增函数,则![]() ,解得
,解得![]()
若![]() 在
在上为减函数,则
![]() ,解得
,解得![]()
综上可知,![]() 的取值范围为
的取值范围为![]() 或
或![]()
(3)假设存在满足条件的![]() ,则
,则![]() 的最大值只可能在
的最大值只可能在![]() 处取得,
处取得,
其中![]()
若![]() ,则有
,则有![]() 得
得![]() 的值不存在,舍去
的值不存在,舍去
若![]() ,则有
,则有![]() ,解得
,解得![]()
而![]() 时,对称轴
时,对称轴![]() ,
,
则最大值应在![]() 处取得,与条件矛盾,舍去
处取得,与条件矛盾,舍去
若![]() ,则
,则![]() ,且
,且![]() ,
,
化简得![]() ,解得
,解得![]() 或
或![]() …(13分)
…(13分)
综上可知,当![]() 或
或![]() 时,函数
时,函数![]() 在
在![]() 上的最大值是4.
上的最大值是4.

练习册系列答案
相关题目
【题目】某校高中三个年级共有学生![]() 名,各年级男生、女生的人数如下表:
名,各年级男生、女生的人数如下表:
高一年级 | 高二年级 | 高三年级 | |
男生 |
|
|
|
女生 |
|
|
|
已知在高中学生中随机抽取一名同学时,抽到高三年级女生的概率为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)现用分层抽样的方法在全校抽取![]() 名学生,则在高二年级应抽取多少名学生?
名学生,则在高二年级应抽取多少名学生?
(Ⅲ)已知![]() ,求高二年级男生比女生多的概率.
,求高二年级男生比女生多的概率.