Question

6．在△ABC中，AB=AC=3，BC=2，求：
（1）△ABC的面积S_△ABC及AC边上的高BE；
（2）△ABC的内切圆的半径r；
（3）△ABC的外接圆的半径R．

Answer 1

分析 （1）根据题意可知△ABC为等腰三角形，根据三角形面积计算公式S=底×高计算三角形面积；
（2）利用等面积，求）△ABC的内切圆的半径r；
（3）利用勾股定理，求△ABC的外接圆的半径R．

解答 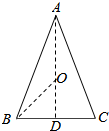解：（1）AB=AC=3，BC=2，作AD⊥BC，则AD为BC边上的高，
∵AB=AC，
∴D为BC边上的中点．
∴AD=2$\sqrt{2}$，
∴S_△ABC=$\frac{1}{2}$×BC×AD=2$\sqrt{2}$．
由S_△ABC=$\frac{1}{2}$×BE×AC=2$\sqrt{2}$，可得BE=$\frac{4\sqrt{2}}{3}$．
（2）由等面积可得S_△ABC=2$\sqrt{2}$=$\frac{1}{2}$（3+3+2）r，∴r=$\frac{\sqrt{2}}{2}$；
（3）由勾股定理可得R²=（2$\sqrt{2}$-R）²+1²，∴R=$\frac{9\sqrt{2}}{8}$．

点评 本题考查了勾股定理的运用，考查了等腰三角形的高线即中线的性质，解本题的关键是掌握等腰三角形底边的高线，中线，角平分线三线合一的性质．