Question

【题目】某艺术品公司欲生产一款迎新春工艺礼品，该礼品是由玻璃球面和该球的内接圆锥组成，圆锥的侧面用于艺术装饰，如图1.为了便于设计，可将该礼品看成是由圆及其内接等腰三角形绕底边上的高所在直线旋转180°而成，如图2.已知圆的半径为，设，圆锥的侧面积为.

（1）求关于的函数关系式；

（2）为了达到最佳观赏效果，要求圆锥的侧面积最大.求取得最大值时腰的长度.

Answer 1

【答案】（1） ，（2）侧面积取得最大值时，等腰三角形的腰的长度为

【解析】试题分析：（1）由条件，，，所以S，；（2）令，所以得，通过求导分析，得在时取得极大值，也是最大值。

试题解析：

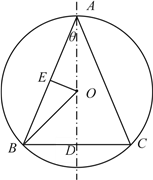
（1）设交于点，过作，垂足为，

在中，，，

在中，，

所以S，

（2）要使侧面积最大，由（1）得：

令，所以得，

由得：

当时，，当时，

所以在区间上单调递增，在区间上单调递减，

所以在时取得极大值，也是最大值；

所以当时，侧面积取得最大值，

此时等腰三角形的腰长

答：侧面积取得最大值时，等腰三角形的腰的长度为．