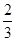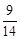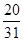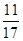题目内容
(本小题满分12分) 设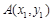 、
、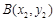 是函数
是函数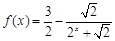 图象上任意两点,且
图象上任意两点,且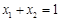 .
.
(Ⅰ)求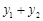 的值;
的值;
(Ⅱ)若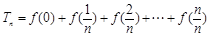 (其中
(其中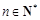 ),求
),求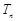 ;
;
(Ⅲ)在(Ⅱ)的条件下,设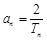 (
(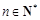 ),若不等式
),若不等式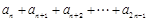 >
>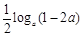 对任意的正整数n恒成立,求实数a的取值范围.
对任意的正整数n恒成立,求实数a的取值范围.
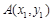 、
、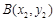 是函数
是函数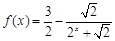 图象上任意两点,且
图象上任意两点,且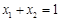 .
.(Ⅰ)求
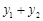 的值;
的值;(Ⅱ)若
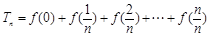 (其中
(其中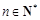 ),求
),求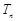 ;
;(Ⅲ)在(Ⅱ)的条件下,设
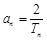 (
(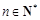 ),若不等式
),若不等式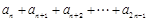 >
>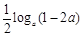 对任意的正整数n恒成立,求实数a的取值范围.
对任意的正整数n恒成立,求实数a的取值范围. (Ⅰ)2;(Ⅱ) .(Ⅲ)
.(Ⅲ)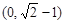 .
.
 .(Ⅲ)
.(Ⅲ)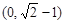 .
. 本试题主要是考查了函数的性质和数列的综合运用。
(1)因为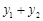
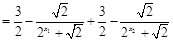
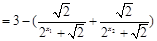 ,通分合并得到结论。
,通分合并得到结论。
(2)由(Ⅰ)可知,当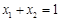 时,
时,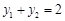 ,
,
由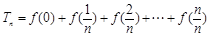 得,
得,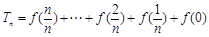 ,然后倒序相加法得到结论。
,然后倒序相加法得到结论。
(3)由(Ⅱ)得,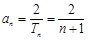 ,不等式
,不等式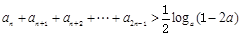 即为
即为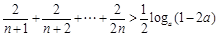 ,运用放缩法得到结论。
,运用放缩法得到结论。
(Ⅰ)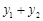
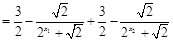
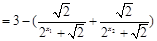
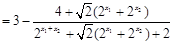
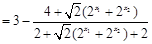
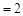 .··········· 4分
.··········· 4分
(Ⅱ)由(Ⅰ)可知,当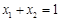 时,
时,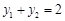 ,
,
由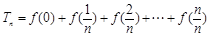 得,
得,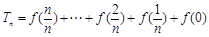 ,
,
∴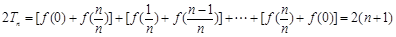 ,
,
∴ .······························· 8分
.······························· 8分
(Ⅲ)由(Ⅱ)得,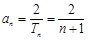 ,不等式
,不等式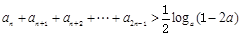 即为
即为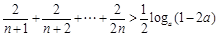 ,设
,设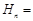
 ,
,
则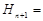
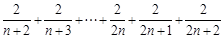 ,
,
∴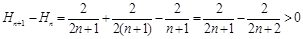 ,
,
∴数列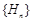 是单调递增数列,∴
是单调递增数列,∴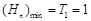 ,··············· 10分
,··············· 10分
要使不等式恒成立,只需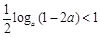 ,即
,即 ,
,
∴ 或
或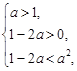 解得
解得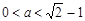 .
.
故使不等式对于任意正整数n恒成立的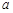 的取值范围是
的取值范围是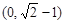 .········ 12分
.········ 12分
(1)因为
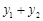
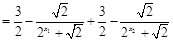
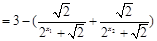 ,通分合并得到结论。
,通分合并得到结论。(2)由(Ⅰ)可知,当
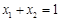 时,
时,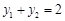 ,
,由
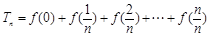 得,
得,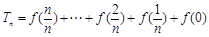 ,然后倒序相加法得到结论。
,然后倒序相加法得到结论。(3)由(Ⅱ)得,
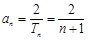 ,不等式
,不等式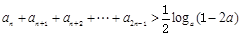 即为
即为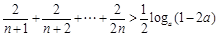 ,运用放缩法得到结论。
,运用放缩法得到结论。(Ⅰ)
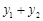
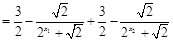
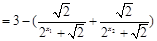
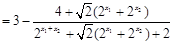
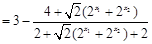
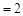 .··········· 4分
.··········· 4分(Ⅱ)由(Ⅰ)可知,当
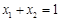 时,
时,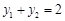 ,
,由
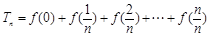 得,
得,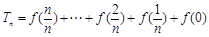 ,
,∴
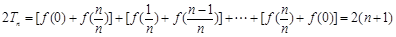 ,
,∴
 .······························· 8分
.······························· 8分(Ⅲ)由(Ⅱ)得,
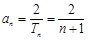 ,不等式
,不等式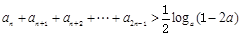 即为
即为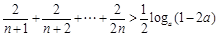 ,设
,设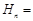
 ,
,则
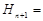
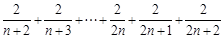 ,
,∴
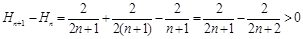 ,
,∴数列
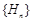 是单调递增数列,∴
是单调递增数列,∴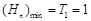 ,··············· 10分
,··············· 10分要使不等式恒成立,只需
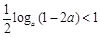 ,即
,即 ,
,∴
 或
或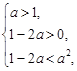 解得
解得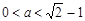 .
.故使不等式对于任意正整数n恒成立的
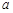 的取值范围是
的取值范围是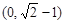 .········ 12分
.········ 12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
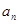 }的前n项和为
}的前n项和为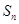 , 满足
, 满足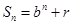 (
(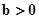
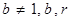 均为常数)
均为常数)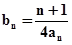
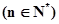 ,求数列
,求数列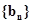 的前
的前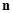 项的和
项的和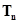 .(6分)
.(6分)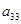 =________________
=________________
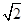
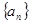 的公差为2,若
的公差为2,若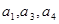 成等比数列, 则
成等比数列, 则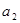 = ( )
= ( )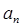 }的前n项和
}的前n项和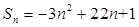 ,
,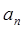 |}的前n项和
|}的前n项和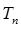 .
. 的前
的前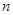 项和为
项和为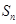 ,
,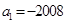 ,若
,若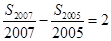
 .
.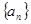 中,若
中,若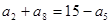 ,则
,则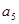 等于 ( )
等于 ( ) 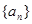 和
和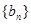 的前n项和分别为
的前n项和分别为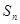 和
和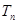 ,对一切自然数n,都有
,对一切自然数n,都有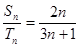 ,则
,则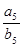 等于 ( )
等于 ( )