题目内容
已知 (a,b∈R,i为虚数单位),那么a+bi的共轭复数为________.
(a,b∈R,i为虚数单位),那么a+bi的共轭复数为________.
-3-i
分析:利用两个复数代数形式的除法法则化简已知的条件可得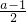 +
+ =-2+bi,再由两个复数相等的充要条件可得得
=-2+bi,再由两个复数相等的充要条件可得得 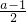 =-2,
=-2, =b,解得 a和 b的值,可得a+bi 的值,从而得到a+bi的共轭复数.
=b,解得 a和 b的值,可得a+bi 的值,从而得到a+bi的共轭复数.
解答:∵ ,(a,b∈R,i为虚数单位),∴
,(a,b∈R,i为虚数单位),∴ ,∴
,∴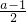 +
+ =-2+bi.
=-2+bi.
由两个复数相等的充要条件可得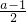 =-2,
=-2, =b,解得 a=-3,b=1.
=b,解得 a=-3,b=1.
∴a+bi=-3+i,a+bi的共轭复数为-3-i,
故答案为:-3-i.
点评:本题主要考查两个复数代数形式的除法,两个复数相等的充要条件,共轭复数的定义,求出 a=-3,b=1,是解题的关键.
分析:利用两个复数代数形式的除法法则化简已知的条件可得
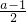 +
+ =-2+bi,再由两个复数相等的充要条件可得得
=-2+bi,再由两个复数相等的充要条件可得得 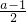 =-2,
=-2, =b,解得 a和 b的值,可得a+bi 的值,从而得到a+bi的共轭复数.
=b,解得 a和 b的值,可得a+bi 的值,从而得到a+bi的共轭复数.解答:∵
 ,(a,b∈R,i为虚数单位),∴
,(a,b∈R,i为虚数单位),∴ ,∴
,∴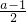 +
+ =-2+bi.
=-2+bi.由两个复数相等的充要条件可得
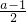 =-2,
=-2, =b,解得 a=-3,b=1.
=b,解得 a=-3,b=1.∴a+bi=-3+i,a+bi的共轭复数为-3-i,
故答案为:-3-i.
点评:本题主要考查两个复数代数形式的除法,两个复数相等的充要条件,共轭复数的定义,求出 a=-3,b=1,是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (a,b∈R,i为虚数单位),则a,b的值分别为
(a,b∈R,i为虚数单位),则a,b的值分别为 ,-1
,-1
 ,
, (a,b∈R,i为虚数单位),那么a+bi的共轭复数为 .
(a,b∈R,i为虚数单位),那么a+bi的共轭复数为 . (a,b∈R,i为虚数单位),则a+b= .
(a,b∈R,i为虚数单位),则a+b= . (a,b∈R,i为虚数单位),则a,b的值分别为( )
(a,b∈R,i为虚数单位),则a,b的值分别为( ) ,-1
,-1 ,
,
 ,
,