题目内容
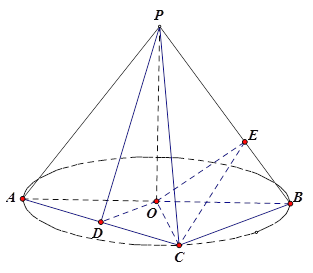
【题目】(本题满分12分)如图, ![]() 是圆
是圆![]() 的直径,点
的直径,点![]() 是圆
是圆![]() 上异于
上异于![]() 的点,
的点, ![]() 垂直于圆
垂直于圆![]() 所在的平面,且
所在的平面,且![]() .
.
(Ⅰ)若![]() 为线段
为线段![]() 的中点,求证
的中点,求证![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 体积的最大值;
体积的最大值;
(Ⅲ)若![]() ,点
,点![]() 在线段
在线段![]() 上,求
上,求![]() 的最小值.
的最小值.
【答案】(Ⅰ)详见解析;(Ⅱ) ![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】解法一:(Ⅰ)在![]() 中,因为
中,因为![]() ,
, ![]() 为
为![]() 的中点,
的中点,
所以![]() .又
.又![]() 垂直于圆
垂直于圆![]() 所在的平面,所以
所在的平面,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅱ)因为点![]() 在圆
在圆![]() 上,
上,
所以当![]() 时,
时, ![]() 到
到![]() 的距离最大,且最大值为
的距离最大,且最大值为![]() .
.
又![]() ,所以
,所以![]() 面积的最大值为
面积的最大值为![]() .
.
又因为三棱锥![]() 的高
的高![]() ,故三棱锥
,故三棱锥![]() 体积的最大值为
体积的最大值为![]() .
.
(Ⅲ)在![]() 中,
中, ![]() ,
, ![]() ,所以
,所以![]() .
.
同理![]() ,所以
,所以![]() .
.
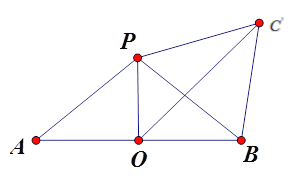
在三棱锥![]() 中,将侧面
中,将侧面![]() 绕
绕![]() 旋转至平面
旋转至平面![]() ,使之与平面
,使之与平面![]() 共面,如图所示.
共面,如图所示.
当![]() ,
, ![]() ,
, ![]() 共线时,
共线时, ![]() 取得最小值.
取得最小值.
又因为![]() ,
, ![]() ,所以
,所以![]() 垂直平分
垂直平分![]() ,
,
即![]() 为
为![]() 中点.从而
中点.从而![]() ,
,
亦即![]() 的最小值为
的最小值为![]() .
.
解法二:(Ⅰ)、(Ⅱ)同解法一.
(Ⅲ)在![]() 中,
中, ![]() ,
, ![]() ,
,
所以![]() ,
, ![]() .同理
.同理![]() .
.
所以![]() ,所以
,所以![]() .
.
在三棱锥![]() 中,将侧面
中,将侧面![]() 绕
绕![]() 旋转至平面
旋转至平面![]() ,使之与平面
,使之与平面![]() 共面,如图所示.
共面,如图所示.
当![]() ,
, ![]() ,
, ![]() 共线时,
共线时, ![]() 取得最小值.
取得最小值.
所以在![]() 中,由余弦定理得:
中,由余弦定理得:
![]()
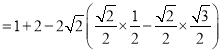
![]() .
.
从而![]() .
.
所以![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
相关题目
【题目】有编号为![]() 的10个零件,测量其直径(单位:cm),得到下面数据:
的10个零件,测量其直径(单位:cm),得到下面数据:
编号 |
|
|
|
|
|
|
|
|
|
|
直径 | 1.51 | 1.49 | 1.49 | 1.51 | 1.49 | 1.51 | 1.47 | 1.46 | 1.53 | 1.47 |
其中直径在区间![]() 内的零件为一等品.
内的零件为一等品.
(1)上述10个零件中,随机抽取1个,求这个零件为一等品的概率.
(2)从一等品零件中,随机抽取2个;
①用零件的编号列出所有可能的抽取结果;
②求这2个零件直径相等的概率.