题目内容
如图,在直三棱柱ABC—A1B1C1中,∠ACB=90°,AC=BC=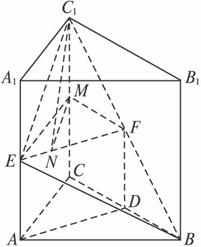
(1)求证:EF∥底面ABC.
(2)求平面EBC1与底面ABC所成的锐二面角的大小.
答案:方法一:(1)证明:取BC的中点D,连结AD、DF.

∵F为BC1的中点,∴DF∥CC1∥AE,DF=![]() CC1=
CC1=![]() AA1=AE.∴四边形EADF为平行四边形.∴EF∥AD.又AD
AA1=AE.∴四边形EADF为平行四边形.∴EF∥AD.又AD![]() 底面ABC,∴EF∥底面ABC.
底面ABC,∴EF∥底面ABC.
(2)解:取CC1的中点M,连结EM、FM,则EM∥AC,FM∥BC,∴平面EFM∥底面ABC.∴平面EBC1与底面所成的锐二面角等于平面EBC1与平面EFM所成的锐二面角.作MN⊥EF于N,连结C1N,则EF⊥C1N,∠C1NM为平面EBC1与平面EFM所成的锐二面角的平面角.
在Rt△EMF中,EM=![]() ,MF=
,MF=![]() ,EF=15+
,EF=15+![]() ,∴MN=
,∴MN=![]() .
.
又C1M=3,∴在Rt△C1MN中,tan∠C1NM=![]() .∴∠C1NM=60°,即所求锐二面角的大小为60°.
.∴∠C1NM=60°,即所求锐二面角的大小为60°.
方法二:(1)证明:以C为原点,CA为x轴,CB为y轴,CC1为z轴建立空间直角坐标系,
则A(![]() ,0,0),B(0,
,0,0),B(0,![]() ,0),C(0,0,6),E(
,0),C(0,0,6),E(![]() ,0,3),F(0,
,0,3),F(0,![]() ,3),取BC中点D,则D(0,
,3),取BC中点D,则D(0,![]() ,0),
,0),
∴![]() =(-
=(-![]() ,
,![]() ,0),
,0),![]() =(-
=(-![]() ,
,![]() ,0).∴
,0).∴![]() =
=![]() .∴EF∥平面ABC.
.∴EF∥平面ABC.
(2)解:设平面EBC1的法向量为n=(x,y,z),又BE=(![]() ,-
,-![]() ,3),
,3),
由n⊥![]() ,得n·
,得n·![]() =0,即
=0,即![]() x-
x-![]() y+3z=0;①
y+3z=0;①
由n⊥![]() ,得n·
,得n·![]() =0,即-
=0,即-![]() x+
x+![]() y+0·z=0.②
y+0·z=0.②
由①②知可取n=(3,6,![]() ).
).
又平面ABC的一个法向量为m=(0,0,1),
∴cos〈m,n〉=![]() .
.
∴〈m,n〉=60°.
∴所求锐二面角的大小为60°.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目




