题目内容
已知两个非零向量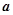 与
与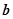 ,定义
,定义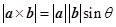 ,其中
,其中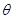 为
为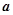 与
与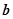 的夹角.若
的夹角.若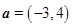 ,
, 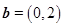 ,则
,则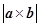 的值为 ( )
的值为 ( )
A.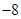 | B.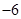 | C.8 | D.6 |
D
解析试题分析:根据题意 ,所以
,所以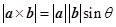
 .
.
考点:平面向量的坐标运算.

练习册系列答案
相关题目
若非零向量 满足
满足 //
// ,且
,且 ,则
,则 ( )
( )
| A.4 | B.3 | C.2 | D.0 |
已知向量 ,
, ,
, ,若
,若 ,则实数
,则实数 的值为( )
的值为( )
A. | B. | C. | D. |
在 所在的平面内,点
所在的平面内,点 满足
满足
 ,
, ,且对于任意实数
,且对于任意实数 ,恒有
,恒有
 , 则( )
, 则( )
A. | B. | C. | D. |
若等边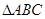 的边长为
的边长为 ,平面内一点
,平面内一点 满足
满足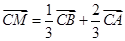 ,则
,则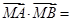 ( )
( )
A.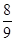 | B.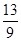 | C.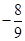 | D.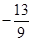 |
已知向量a=(cosθ,sinθ),向量b=( ,-1),则|2a-b|的最大值,最小值分别是( )
,-1),则|2a-b|的最大值,最小值分别是( )
A.4 ,0 ,0 | B.4,4 | C.16,0 | D.4,0 |
已知 ,
, ,点
,点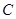 满足
满足 (
( ),且
),且 ,则
,则 等于
等于
A. | B.1 | C. | D. |
 ,若
,若 ,且
,且 ,则用阴影表示
,则用阴影表示 点所有可能的位置区域正确的是 ( )
点所有可能的位置区域正确的是 ( )
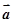 是已知的平面向量且
是已知的平面向量且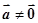 ,关于向量
,关于向量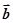 ,总存在向量
,总存在向量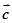 ,使
,使 ;
;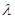 和
和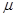 ,使
,使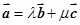 ;
;