Question

已知△ABC为正三角形，AE与CD都垂直于平面ABC，且AE=AB=2a,CD=a，F为BE的中点.

（1）求证：DF//平面ABC；

（2）求证：AF⊥BE.

Answer 1

思路分析：当两个空间向量数量积为0时，两向量相互垂直.

解：（1）以A为原点，AB为x轴，AE为z轴建立坐标系，

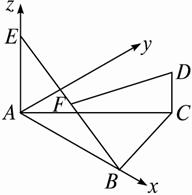
    则B(2a,0,0)，E(0,0,2a)，D(2a,,a)，F(a,0,a).

=(-a,,0)，=(0,0,2a).

∵=0，∴⊥.

    又AE⊥平面ABC，∴//平面ABC.

(2)∵=(a,0,a),=(-2a,0,2a)，

∴=0.

∴⊥.

方法归纳 用两个空间向量数量积为0来判断两向量相互垂直，是向量在立体几何中运用的一个重要的手段.