Question

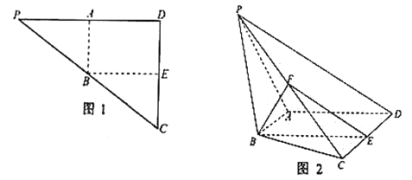
【题目】如图,四棱柱中,底面是等腰梯形, ,,是线段的中点,平面.

(1)求证:平面；

(2)若,求平面和平面所成的锐二面角的余弦值.

Answer 1

【答案】（1）证明见解析；（2）.

【解析】分析：（1）以为坐标原点建立空间直角坐标系，写出相应点的坐标，即可通过线面垂直的判定方法证得平面；

（2）写出相应点的坐标，求出平面的一个法向量和平面的一个法向量，即可求得答案.

详解：(1)证明方法一: 连接，因为底面是等腰梯形且

所以，，又因为是的中点，

因此，且，

所以，且，

又因为且，

所以，

因为，平面，

所以平面，

所以，平面平面，

在平行四边形中，因为,

所以平行四边形是菱形，

因此，

所以平面.

解法二：底面是等腰梯形，,,

所以，，

因此，

以为坐标原点建立空间直角坐标系，则,，

由得，

所以,,,，

因此，且，

所以且，

所以，平面.

(2)底面是等腰梯形，,,

所以，，

因此，

以为坐标原点建立空间直角坐标系，则,,,，

所以，,，

设平面的一个法向量，

由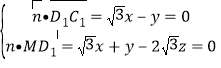得，

由是平面的法向量，

因此，

平面和平面所成的锐二面角的余弦值是.