题目内容
已知椭圆C：
=1（a＞b＞0）的长轴长为4，且离心率e=
．
（I）求椭圆的方程
（II）椭圆C：=1（a＞b＞0）的左顶点为A，右顶点为B，点S是椭圆C上位于x轴上方的动点，直线AS，BS与直线l：x=3分别交于M，N两点，求线段MN的长度的最小值．
解：（I）由题设可得2a=4，
=
∴a=2，c=
∴b2=a2-c2=2
∴椭圆的方程为
；
（II）由题意，直线AS的斜率k存在，且k＞0，故可设AS的方程为y=k（x+2），代入椭圆方程，
可得（1+2k2）x2+8k2x+8k2-4=0
设S（x1，y1），则（-2）×x1=
，∴
，∴
∵B（2，0），可得SB的方程为
化简可得
由
，可得
，∴N（3，
）
故|MN|=|
|
∵k＞0，∴|MN|=≥
当且仅当5k=
，即k=
时等号成立
∴k=时，线段MN的长度的最小值为．
分析：（I）利用椭圆的长轴长为4，且离心率e=，求出几何量，从而可得椭圆的方程；
（II）设出AS的方程代入椭圆方程，利用韦达定理，确定S的坐标，从而可得SB的方程，与直线x=3联立，求出N的坐标，进而可得|MN|，利用基本不等式，可得结论．
点评：本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查韦达定理的运用，考查基本不等式的运用，属于中档题．
=∴a=2，c=
∴b2=a2-c2=2
∴椭圆的方程为
；（II）由题意，直线AS的斜率k存在，且k＞0，故可设AS的方程为y=k（x+2），代入椭圆方程，
可得（1+2k2）x2+8k2x+8k2-4=0
设S（x1，y1），则（-2）×x1=
，∴，∴∵B（2，0），可得SB的方程为
化简可得
由
，可得，∴N（3，）故|MN|=|
|∵k＞0，∴|MN|=
≥当且仅当5k=
，即k=时等号成立∴k=
时，线段MN的长度的最小值为．分析：（I）利用椭圆的长轴长为4，且离心率e=
，求出几何量，从而可得椭圆的方程；（II）设出AS的方程代入椭圆方程，利用韦达定理，确定S的坐标，从而可得SB的方程，与直线x=3联立，求出N的坐标，进而可得|MN|，利用基本不等式，可得结论．
点评：本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查韦达定理的运用，考查基本不等式的运用，属于中档题．
练习册系列答案
相关题目
+
=1（a＞b＞0）经过（1，1）与（
，
）两点．
+
+
为定值．
已知椭圆C：
+
=1（a＞b＞0）的左右焦点为F1，F2，过F2线与圆x2+y2=b2相切于点A，并与椭圆C交与不同的两点P，Q，如图，PF1⊥PQ，若A为线段PQ的靠近P的三等分点，则椭圆的离心率为（ ）
+
=1（a＞b＞0），直线l为圆O：x2+y2=b2的一条切线，记椭圆C的离心率为e．
，且恰好经过椭圆的右顶点，求e的大小；
y+3=0相切，求椭圆方程．
+
=1（a＞b＞0），直线l为圆O：x2+y2=b2的一条切线，记椭圆C的离心率为e．
，且恰好经过椭圆的右顶点，求e的大小；
y+3=0相切，求椭圆方程．
=1（a>b>0）的离心率为
，且在x轴上的顶点分别为
：
与
轴交于点T，P为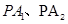
分别与椭圆交于M、N两点，试问直线MN是否通过椭圆的焦点？并证明你的结论.