题目内容
在极坐标系中,已知圆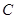 的圆心
的圆心 ,半径
,半径 .
.
(Ⅰ)求圆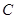 的极坐标方程;
的极坐标方程;
(Ⅱ)若 ,直线
,直线 的参数方程为
的参数方程为 (
( 为参数),直线
为参数),直线 交圆
交圆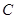 于
于 两点,求弦长
两点,求弦长 的取值范围.
的取值范围.
①. .②.
.②. .
.
解析试题分析:(Ⅰ) 先建立圆的直角坐标方程,再化成极坐标方程,或直接建立极坐标方程. (Ⅱ)直线参数方程中参数的几何意义及应用于求弦长,再运用三角函数求范围.
试题解析:(Ⅰ)【法一】∵ 的直角坐标为
的直角坐标为 ,
,
∴圆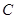 的直角坐标方程为
的直角坐标方程为 .
.
化为极坐标方程是 .
.
【法二】设圆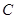 上任意一点
上任意一点 ,则
,则
如图可得, .
.
化简得 4分
4分
(Ⅱ)将 代入圆
代入圆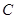 的直角坐标方程
的直角坐标方程 ,
,
得
即
有 .
.
故 ,
,
∵ ,
,
∴ ,
,
即弦长 的取值范围是
的取值范围是 10分
10分
考点:1.极坐标与直角坐标之间的互化;2.极坐标系下建立曲线方程;3.直线参数方程的应用;4.三角函数求值域.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,以
中,以 为极点,
为极点,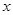 轴非负半轴为极轴建立坐标系,已知曲线
轴非负半轴为极轴建立坐标系,已知曲线 的极坐标方程为
的极坐标方程为 ,直线
,直线 的参数方程为:
的参数方程为: (
( 为参数),两曲线相交于
为参数),两曲线相交于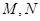 两点.
两点. 求
求 的值.
的值. 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线
 ,过点
,过点 的直线
的直线 的参数方程为:
的参数方程为:
 ,(t为参数),直线
,(t为参数),直线 分别交于
分别交于 两点.
两点.  成等比数列,求
成等比数列,求 的值.
的值.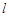 的参数方程为
的参数方程为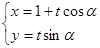 (t为参数,0<a<
(t为参数,0<a<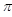 ),曲线C的极坐标方程为
),曲线C的极坐标方程为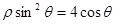 .
. 为参数).以O为极点,
为参数).以O为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系. 的极坐标方程是
的极坐标方程是 ,射线
,射线 与圆C的交点为O,P,与直线
与圆C的交点为O,P,与直线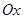 中,直线
中,直线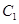 的极坐标方程为
的极坐标方程为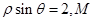 是
是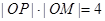 ,记点P的轨迹为
,记点P的轨迹为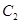 。
。 距离的最大值。
距离的最大值。 的参数方程为
的参数方程为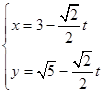 (t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 .
. ,求|PA|+|PB|.
,求|PA|+|PB|. 为极点,以
为极点,以 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线 ,过点
,过点 的直线
的直线 的参数方程为
的参数方程为 ,设直线
,设直线 与曲线
与曲线 分别交于
分别交于 ;
; 的普通方程;
的普通方程; 成等比数列,求
成等比数列,求 的值.
的值. .
.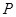 是圆
是圆 上一动点,点
上一动点,点 满足
满足 ,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.