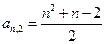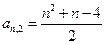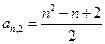题目内容
(本小题满分12分)数列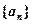 的前n项和为
的前n项和为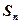 ,且满足
,且满足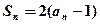 ,
,
数列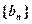 中,
中,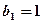 ,且点
,且点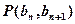 在直线
在直线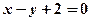 上,
上,
(1)求数列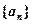 、
、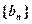 的通项公式;
的通项公式;
(2)设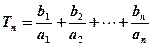 , 求
, 求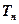 ;
;
(3)设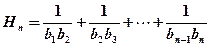 ,求使得
,求使得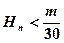 对所有的
对所有的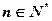 都成立的最小正整数
都成立的最小正整数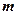 .
.
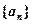 的前n项和为
的前n项和为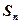 ,且满足
,且满足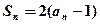 ,
,数列
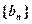 中,
中,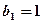 ,且点
,且点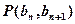 在直线
在直线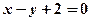 上,
上,(1)求数列
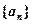 、
、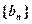 的通项公式;
的通项公式;(2)设
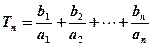 , 求
, 求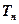 ;
; (3)设
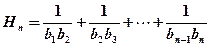 ,求使得
,求使得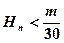 对所有的
对所有的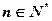 都成立的最小正整数
都成立的最小正整数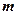 .
. (1)
 ,
,
(2)

(3)

解:(1) ,
,
相减得: ,又
,又
 -------2分
-------2分
又 在直线
在直线 上,
上, ,又
,又
 -------------------4分
-------------------4分
(2)

相减得: ------------------6分
------------------6分
化简得 ---------------------8分
---------------------8分
(3)

 --------------------10分
--------------------10分
要使 所有的
所有的 都成立,必须且仅需满足
都成立,必须且仅需满足
所以满足要求的最小正整数为 . -----------------------------------12分
. -----------------------------------12分
 ,
,
相减得:
 ,又
,又
 -------2分
-------2分又
 在直线
在直线 上,
上, ,又
,又
 -------------------4分
-------------------4分 (2)


相减得:
 ------------------6分
------------------6分化简得
 ---------------------8分
---------------------8分(3)


 --------------------10分
--------------------10分要使
 所有的
所有的 都成立,必须且仅需满足
都成立,必须且仅需满足
所以满足要求的最小正整数为
 . -----------------------------------12分
. -----------------------------------12分
练习册系列答案
相关题目
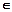
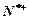 )且a3+
)且a3+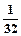 是a2,a4的等差中项,数列{bn}的前n项和Sn=n2
是a2,a4的等差中项,数列{bn}的前n项和Sn=n2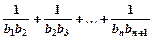 ,求证:Tn<
,求证:Tn<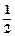
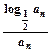 ,T/n=c1+c2+…+cn,求使T/n+n
,T/n=c1+c2+…+cn,求使T/n+n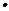 2n+1>125成立的正整数n的最小值
2n+1>125成立的正整数n的最小值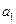 =2,且2,an,Sn成等差数列。
=2,且2,an,Sn成等差数列。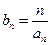 ,求数列{
,求数列{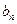 }的前n项和Tn;
}的前n项和Tn;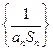 的前n项和为
的前n项和为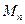 ,求证:
,求证: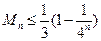 .
.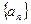 的前
的前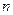 项和为
项和为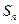 ,且
,且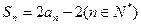 ,数列
,数列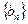 中,
中,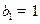 ,
,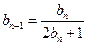 .(
.(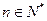 )
)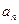 和
和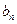
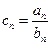 ,求数列
,求数列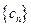 的前n项和
的前n项和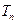 .
.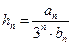 ,若对于一切
,若对于一切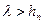 恒成立,求
恒成立,求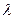 的取值范围
的取值范围 是等差数列
是等差数列 的前n项和,且
的前n项和,且 的值为
的值为 的前
的前 项和为
项和为 ,若
,若 ,则
,则 的值是
的值是  的前n项的和Sn=3n2+ n,则此数列的通项公式a n=__ .
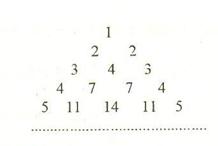
的前n项的和Sn=3n2+ n,则此数列的通项公式a n=__ .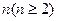 按右图方式构成三角形数表:第一行依次写上数1,2,3,……n,在下面一行的每相邻两个数的正中间上方写上这两个数之和,得到上面一行的数(比
按右图方式构成三角形数表:第一行依次写上数1,2,3,……n,在下面一行的每相邻两个数的正中间上方写上这两个数之和,得到上面一行的数(比
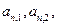 ……
……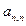 (n=1,2,3…………)分别表示第n行的第一个数,第二个数,……第n个数.则
(n=1,2,3…………)分别表示第n行的第一个数,第二个数,……第n个数.则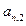 (n
(n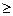 2且n
2且n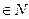 )的表达式
)的表达式