题目内容

15．已知函数$\left\{{\begin{array}{l}{{x^2}+1，x≤0}\\{\sqrt{x}，x＞0}\end{array}}\right.$，则f（f（-2））=$\sqrt{5}$．

分析 直接利用分段函数，逐步由里及外求解即可．

解答 解：函数$\left\{{\begin{array}{l}{{x^2}+1，x≤0}\\{\sqrt{x}，x＞0}\end{array}}\right.$，
则f（f（-2））=f（（-2）2+1）=f（5）=$\sqrt{5}$．
故答案为：$\sqrt{5}$．

点评 本题考查分段函数的应用，函数值的求法，考查计算能力．

练习册系列答案
相关题目
5．已知f（x）=$\frac{1-x}{1+x}$．
（1）求f（f（2）））的值；
（2）若实数a满足f（a2）=$-\frac{3}{5}$，且lg2a-1＜0，求a的值；
（3）设函数f1（x）=f（x）=$\frac{1-x}{1+x}$（x≠-1），对于一切正整数n，都有fn+1（x）=f1（fn（x）），且f3（x）=f4（x），求f2012（x）的值；
（4）设函数φ（x）=$\frac{1+x}{x-1}|x-2{|}^{\frac{1}{2}}$（x≠1），若函数g（x）=f（x）•φ（x），t=a2-2a+$\frac{13}{3}$（a∈R），试判断g（1.2），g（2.5），g（t）的大小关系．（请按由大到小的顺序排）
6．用更相减损术得111与148的最大公约数为（　　）
A．1B．17C．23D．37
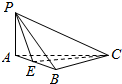3．如图，三棱锥P-ABC中，△PAB是正三角形，E是AB的中点，AB⊥BC，平面PAB⊥平面ABC．若AB=2，BC=$\sqrt{2}$，则点A到平面PEC的距离是$\frac{\sqrt{6}}{3}$．
10．已知，命题p：?x∈R，x2+ax+2≥0，命题q：?x∈[-3，-$\frac{1}{2}$]，x2-ax+1=0．
（1）若命题p为真命题，求实数a的取值范围；
（2）若命题q为真命题，求实数a的取值范围；
（3）若命题“p∨q”为真命题，且命题“p∧q”为假命题，求实数a的取值范围．
20．已知函数f（x）=x|x-m|，x∈R，且f（4）=0．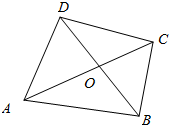
（1）求实数m的值；
（2）作出函数f（x）的图象并直接写出f（x）单调减区间．
7．函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+4x，x≤-2}\\{\frac{x}{2}．x＞-2}\end{array}\right.$的定义域为R，值域为[-4，+∞）．
4．如图所示，在四边形ABCD中，$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$，对角线AC与BD交于点O，设$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，用$\overrightarrow{a}$和$\overrightarrow{b}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$．
5．已知点P（0，-1）在角α的终边上，则所有角α组成的集合S={α|α=$\frac{3π}{2}$+2kπ，k∈Z}．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网