题目内容
(2012•绵阳一模)已知函数f(x)=
则满足不等式f(x2-3)<f(2x)中x的取值范围为( )
|
分析:对f(x2-3)<f(2x)进行等价转化,利用函数f(x)的单调性去掉不等式中的符号“f”,转化为x2-3与2x的不等式即可解得.
解答:解:不等式f(x2-3)<f(2x)等价于
或
,
解得0<x≤
,或
<x<3.所以x的取值范围为(0,3).
故选A.
|
|
解得0<x≤
| 3 |
| 3 |
故选A.
点评:本题考查了应用函数的单调性解不等式.解决该题的技巧在于用单调性对不等式进行等价转化,若把不等式表示出来再解则复杂得多.

练习册系列答案
相关题目
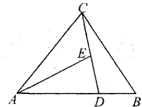 (2012•绵阳一模)如图,在△ABC中,AD=2DB,DE=EC,若
(2012•绵阳一模)如图,在△ABC中,AD=2DB,DE=EC,若