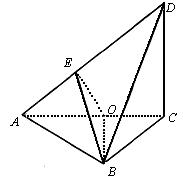
题目内容
已知平面四边形ABCD中，AB=BC=
，ÐBAC=45°，ÐACD=90°，ÐADC=60°，把四边形沿对角线AC折成直二面角，并连结BD．
（1）求证：平面ABC^平面BCD；
（2）求平面ABD与平面ACD所成二面角的平面角的正切值．
答案：
解析：
解析：
| （1）∵ 平面ABC^平面ACD，CD^AC，∴ CD^平面ABC ∴ CD^AB 又BC^AB∴AB^平面BCD，故平面ABC^平面BCD． （2）在平面ABC内作BO^AC，垂足为O，∵ 平面ABC^平面ACD ∴ BO^平面ACD在平面ACD内作OE^AD，垂足为E，连结BE，则BE^AD ∴ ÐBEO为平面ABD与平面ACD所成二面角的平面角．
在RtDBOE中，BO=
|
，
∴ 
练习册系列答案
相关题目
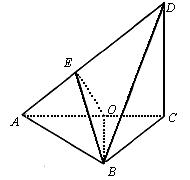
已知平面四边形ABCD的对角线AC，BD交于点O，AC⊥BD，且BA=BC=4，DA=DC=2
如图，已知空间四边形ABCD中，BC=AC，AD=BD，E是AB的中点，求证：
,求P到直线BC的距离;