题目内容
已知圆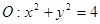 和点
和点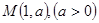 (1)若过点
(1)若过点 有且只有一条直线与圆
有且只有一条直线与圆 相切,求正实数
相切,求正实数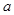 的值,并求出切线方程;(2)若
的值,并求出切线方程;(2)若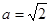 ,过点
,过点 的圆的两条弦
的圆的两条弦 互相垂直,设
互相垂直,设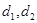 分别为圆心到弦
分别为圆心到弦 的距离.
的距离.
(Ⅰ)求 的值;
的值;
(Ⅱ)求两弦长之积 的最大值.
的最大值.
【答案】
(Ⅰ)3(Ⅱ)10
【解析】
试题分析:本题第(1)问,本题考查的是圆的切线方程,即直线与圆方程的应用.(要求过点M的切线l的斜率,关键是求出切点坐标,由M点也在圆上,故满足圆的方程,则易求M点坐标,然后代入圆的切线方程,整理即可得到答案;
第(2)问,由基本不等式可求出两弦长之积 的最大值.
的最大值.
解:(1)
 得
得

∴切线方程为 即
即
(Ⅰ)当 都不过圆心时,
都不过圆心时,
设 于
于 ,则
,则 为矩形,
为矩形,

当 中有一条过圆心时,上式也成立
中有一条过圆心时,上式也成立
(Ⅱ)
∴ 

(当且仅当 时等号成立)
时等号成立)
考点:直线和圆的方程的应用;点与圆的位置关系.
点评:本题考查直线和圆的方程的应用,着重考查分类讨论思想与转化思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 和点
和点
 有且只有一条直线与圆
有且只有一条直线与圆 相切,求实数
相切,求实数 的值,并求出切线方程;
的值,并求出切线方程; ,过点
,过点 ,且
,且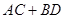 的最大值。
的最大值。 (3)设
(3)设 (3)设
(3)设