题目内容
已知圆![]()
![]() 和点
和点![]() .
.
(1)求以点![]() 为圆心,且被
为圆心,且被![]() 轴截得的弦长为
轴截得的弦长为![]() 的圆⊙
的圆⊙![]() 的方程;
的方程;
(2)过点![]() 向圆O引切线
向圆O引切线![]() ,求直线
,求直线![]() 的方程;
的方程;
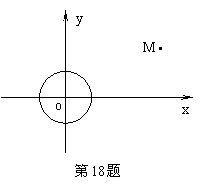 (3)设
(3)设![]() 为⊙
为⊙![]() 上任一点,过点
上任一点,过点![]() 向圆O引切线,切点为Q. 试探究:平面内是否存在一定点
向圆O引切线,切点为Q. 试探究:平面内是否存在一定点![]() ,使得
,使得![]() 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
解:(Ⅰ)设圆的半径为![]() ,则
,则![]() ……………………………………3分
……………………………………3分
∴⊙![]() 的方程为
的方程为![]() ……………………………………………………5分
……………………………………………………5分
(Ⅱ)设切线![]() 方程为
方程为![]() ,易得
,易得![]() ,解得
,解得![]() ……………8分
……………8分
∴切线![]() 方程为
方程为![]() ………………………………………………………10分
………………………………………………………10分
(Ⅲ)假设存在这样的点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,相应的定值为
,相应的定值为![]() ,
,
根据题意可得![]() ,∴
,∴ …………………………12分
…………………………12分
即![]() (*),
(*),
又点![]() 在圆上∴
在圆上∴![]() ,即
,即![]() ,代入(*)式得:
,代入(*)式得:
![]() ………………………………14分
………………………………14分
若系数对应相等,则等式恒成立,∴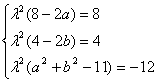 ,
,
解得![]() ,
,
∴可以找到这样的定点![]() ,使得
,使得![]() 为定值. 如点
为定值. 如点![]() 的坐标为
的坐标为![]() 时,比值为
时,比值为![]() ;
;
点![]() 的坐标为
的坐标为![]() 时,比值为
时,比值为![]() …………………………………………………………16分
…………………………………………………………16分

练习册系列答案
相关题目
 及点
及点 .
. 为圆
为圆 上任一点,求
上任一点,求 的最大值和最小值;
的最大值和最小值; ,直线
,直线 与圆C交于点A、B.当
与圆C交于点A、B.当 为何值时
为何值时 取到最小值。
取到最小值。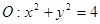 和点
和点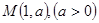 (1)若过点
(1)若过点 有且只有一条直线与圆
有且只有一条直线与圆 相切,求正实数
相切,求正实数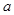 的值,并求出切线方程;(2)若
的值,并求出切线方程;(2)若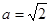 ,过点
,过点 互相垂直,设
互相垂直,设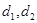 分别为圆心到弦
分别为圆心到弦 的值;
的值; 的最大值.
的最大值. 和点
和点
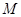 有且只有一条直线与圆
有且只有一条直线与圆 相切,求实数
相切,求实数 的值,并求出切线方程;
的值,并求出切线方程; ,过点
,过点 ,且
,且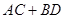 的最大值。
的最大值。 和点
和点 ,若点
,若点 在圆上且
在圆上且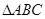 的面积为
的面积为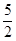 ,则满足条件的点
,则满足条件的点