题目内容
已知A,B是双曲线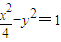 的两个顶点,点P是双曲线上异于A,B的一点,连接PO(O为坐标原点)交椭圆
的两个顶点,点P是双曲线上异于A,B的一点,连接PO(O为坐标原点)交椭圆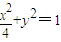 于点Q,如果设直线PA,PB,QA的斜率分别为k1,k2,k3,且
于点Q,如果设直线PA,PB,QA的斜率分别为k1,k2,k3,且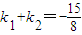 ,假设k3>0,则k3的值为( )
,假设k3>0,则k3的值为( )A.1
B.

C.2
D.4
【答案】分析:由双曲线 可得两个顶点A(-2,0),B(2,0).设P(x,y),则
可得两个顶点A(-2,0),B(2,0).设P(x,y),则 ,可得
,可得 .于是kPA+kPB=
.于是kPA+kPB= =
= =
= .同理设Q(x1,y1),由kOP=kOQ得
.同理设Q(x1,y1),由kOP=kOQ得 .得到kQA+kQB=
.得到kQA+kQB= .可得kPA+kPB+kQA+kQB=0,由
.可得kPA+kPB+kQA+kQB=0,由 ,可得kQA+kQB=
,可得kQA+kQB= .又kQA•kQB=-
.又kQA•kQB=- ,联立解得kQA.
,联立解得kQA.
解答:解:由双曲线 可得两个顶点A(-2,0),B(2,0).设P(x,y),则
可得两个顶点A(-2,0),B(2,0).设P(x,y),则 ,可得
,可得 .
.
∴kPA+kPB= =
= =
= .
.
设Q(x1,y1),则 ,得到
,得到 .
.
由kOP=kOQ得 .
.
∴kQA+kQB= =
= =
= ,
,
∴kPA+kPB+kQA+kQB=0,
∵ ,∴kQA+kQB=
,∴kQA+kQB= …①
…①
又kQA•kQB=- =-
=- …②
…②
联立①②解得kQA=2>0.
故选C.
点评:熟练掌握双曲线、椭圆的标准方程、斜率的计算公式及其有关结论是解题的关键.
 可得两个顶点A(-2,0),B(2,0).设P(x,y),则
可得两个顶点A(-2,0),B(2,0).设P(x,y),则 ,可得
,可得 .于是kPA+kPB=
.于是kPA+kPB= =
= =
= .同理设Q(x1,y1),由kOP=kOQ得
.同理设Q(x1,y1),由kOP=kOQ得 .得到kQA+kQB=
.得到kQA+kQB= .可得kPA+kPB+kQA+kQB=0,由
.可得kPA+kPB+kQA+kQB=0,由 ,可得kQA+kQB=
,可得kQA+kQB= .又kQA•kQB=-
.又kQA•kQB=- ,联立解得kQA.
,联立解得kQA.解答:解:由双曲线
 可得两个顶点A(-2,0),B(2,0).设P(x,y),则
可得两个顶点A(-2,0),B(2,0).设P(x,y),则 ,可得
,可得 .
.∴kPA+kPB=
 =
= =
= .
.设Q(x1,y1),则
 ,得到
,得到 .
.由kOP=kOQ得
 .
.∴kQA+kQB=
 =
= =
= ,
,∴kPA+kPB+kQA+kQB=0,
∵
 ,∴kQA+kQB=
,∴kQA+kQB= …①
…①又kQA•kQB=-
 =-
=- …②
…②联立①②解得kQA=2>0.
故选C.
点评:熟练掌握双曲线、椭圆的标准方程、斜率的计算公式及其有关结论是解题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 的两个顶点,点P是双曲线上异于A,B的一点,连接PO(O为坐标原点)交椭圆
的两个顶点,点P是双曲线上异于A,B的一点,连接PO(O为坐标原点)交椭圆 于点Q,如果设直线PA,PB,QA的斜率分别为k1,k2,k3,且
于点Q,如果设直线PA,PB,QA的斜率分别为k1,k2,k3,且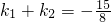 ,假设k3>0,则k3的值为
,假设k3>0,则k3的值为