题目内容
【题目】已知函数![]() ,其中
,其中![]() ,
, ![]() 是自然对数的底数.
是自然对数的底数.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 的单调减区间;
的单调减区间;
(3)若![]() 在
在![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)当
(2)当![]() 时,
时, ![]() 无单调减区间;当
无单调减区间;当![]() 时,
时, ![]() 的单调减区间是
的单调减区间是![]() ;当
;当![]() 时,
时, ![]() 的单调减区间是
的单调减区间是![]() .(3)
.(3)![]()
【解析】试题分析:(1)先对函数解析式进行求导,再借助导数的几何意义求出切线的斜率,运用点斜式求出切线方程;(2)先对函数的解析式进行求导,然后借助导函数的值的符号与函数单调性之间的关系进行分类分析探求;(3)先不等式![]() 进行等价转化,然后运用导数知识及分类整合的数学思想探求函数的极值与最值,进而分析推证不等式的成立求出参数的取值范围。
进行等价转化,然后运用导数知识及分类整合的数学思想探求函数的极值与最值,进而分析推证不等式的成立求出参数的取值范围。
解:(1)因为![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
所以切线方程为![]() .
.
(2) 因为![]() ,
,
当![]() 时,
时, ![]() ,所以
,所以![]() 无单调减区间.
无单调减区间.
当![]() 即
即![]() 时,列表如下:
时,列表如下:

所以![]() 的单调减区间是
的单调减区间是![]() .
.
当![]() 即
即![]() 时,
时, ![]() ,列表如下:
,列表如下:
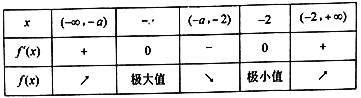
所以![]() 的单调减区间是
的单调减区间是![]() .
.
综上,当![]() 时,
时, ![]() 无单调减区间;
无单调减区间;
当![]() 时,
时, ![]() 的单调减区间是
的单调减区间是![]() ;
;
当![]() 时,
时, ![]() 的单调减区间是
的单调减区间是![]() .
.
(3) ![]() .
.
当![]() 时,由(2)可得,
时,由(2)可得, ![]() 为
为![]() 上单调增函数,
上单调增函数,
所以![]() 在区间
在区间![]() 上的最大值
上的最大值![]() ,符合题意.
,符合题意.
当![]() 时,由(2)可得,要使
时,由(2)可得,要使![]() 在区间
在区间![]() 上恒成立,
上恒成立,
只需![]() ,
, ![]() ,解得
,解得![]() .
.
当![]() 时,可得
时,可得![]() ,
, ![]() .
.
设![]() ,则
,则![]() ,列表如下:
,列表如下:

所以![]() ,可得
,可得![]() 恒成立,所以
恒成立,所以![]() .
.
当![]() 时,可得
时,可得![]() ,无解.
,无解.
综上, ![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
