题目内容
已知在空间四边形OABC中，OB=OC,AB=AC.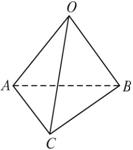
求证：ＯA⊥BC.
证明:∵ＯB=ＯC，AB=AC，ＯA=ＯA,
∴△ＯAC≌△ＯAB.
∴∠AＯC=∠AＯB.
∵
=０,
∴ＯA⊥BC.
启示：利用向量知识证明ＯA⊥BC，就是证明
.因为已知OB=OC(AB=AC),所以
最好用
、
表示(或用
、
表示)，代入
中，根据分配律证得
.
练习册系列答案
相关题目
题目内容
已知在空间四边形OABC中，OB=OC,AB=AC.
求证：ＯA⊥BC.
证明:∵ＯB=ＯC，AB=AC，ＯA=ＯA,
∴△ＯAC≌△ＯAB.
∴∠AＯC=∠AＯB.
∵
=０,
∴ＯA⊥BC.
启示：利用向量知识证明ＯA⊥BC，就是证明.因为已知OB=OC(AB=AC),所以最好用、表示(或用、表示)，代入中，根据分配律证得.
