题目内容
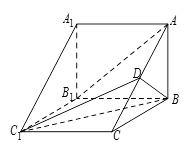
如图,在三棱柱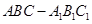 中,侧棱
中,侧棱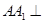 底面
底面 ,
,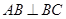 ,
,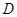 为
为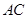 的中点,
的中点,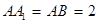 .
.
(Ⅰ)求证: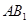 //平面
//平面 ;
;
(Ⅱ)设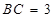 ,求四棱锥
,求四棱锥 的体积.
的体积.
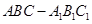 中,侧棱
中,侧棱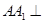 底面
底面 ,
,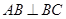 ,
,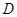 为
为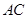 的中点,
的中点,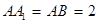 .
.
(Ⅰ)求证:
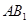 //平面
//平面 ;
;(Ⅱ)设
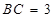 ,求四棱锥
,求四棱锥 的体积.
的体积.(Ⅰ)详见解析;(Ⅱ)体积为3.
试题分析:(Ⅰ)为了证明
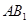 //平面
//平面 ,需要在平面
,需要在平面 内找一条与
内找一条与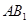 平行的直线,而要找这条直线一般通过作过
平行的直线,而要找这条直线一般通过作过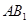 且与平面
且与平面 相交的平面来找.在本题中联系到
相交的平面来找.在本题中联系到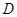 为
为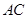 中点,故连结
中点,故连结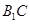 ,这样便得一平面
,这样便得一平面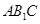 ,接下来只需证
,接下来只需证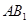 与平面
与平面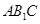 和平面
和平面 的交线平行即可.
的交线平行即可. 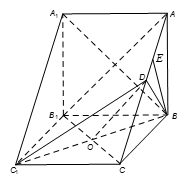
(Ⅱ)底面
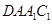 为一直角梯形,故易得其面积,本题的关键是求出点B到平面
为一直角梯形,故易得其面积,本题的关键是求出点B到平面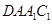 的距离.由于
的距离.由于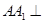 平面
平面 ,所以易得平面
,所以易得平面
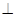 平面
平面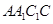 .平面
.平面
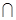 平面
平面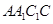
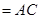 .根据两平面垂直的性质定理知,只需过B作交线AC的垂线即可得点B到平面
.根据两平面垂直的性质定理知,只需过B作交线AC的垂线即可得点B到平面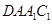 的距离,从而求出体积.
的距离,从而求出体积.试题解析:(Ⅰ)连接
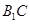 ,设
,设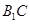 与
与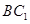 相交于点
相交于点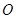 ,连接
,连接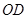 ,
,
∵ 四边形
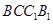 是平行四边形,
是平行四边形,∴点
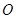 为
为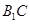 的中点.
的中点.∵
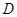 为
为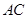 的中点,∴
的中点,∴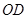 为△
为△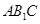 的中位线,
的中位线,∴
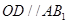 .
.∵
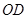
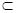 平面
平面 ,
,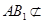 平面
平面 ,
,∴
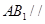 平面
平面 . 6分
. 6分(Ⅱ) ∵
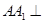 平面
平面 ,
,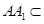 平面
平面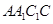 ,
,∴ 平面

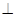 平面
平面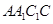 ,且平面
,且平面
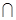 平面
平面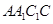
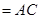 .
.作
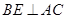 ,垂足为
,垂足为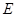 ,则
,则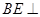 平面
平面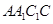 ,
, ∵
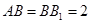 ,
,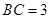 ,
,在Rt△
 中,
中,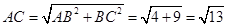 ,
,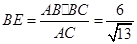 ,
,∴四棱锥
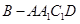 的体积
的体积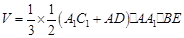
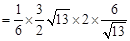
 12分
12分
练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
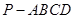 中,底面
中,底面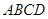 是菱形,
是菱形, ,
, ,
,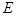 是
是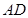 的中点,点
的中点,点 在侧棱
在侧棱 上.
上.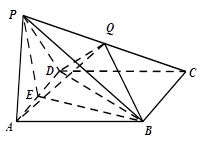
 ;
; //平面
//平面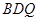 ;
; ,试求
,试求 的值.
的值.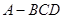 的底面边长为
的底面边长为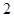 ,侧棱长为
,侧棱长为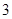 ,
,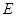 为棱
为棱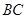 的中点.
的中点.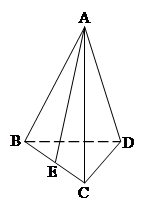
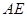 与
与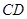 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);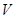 .
.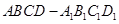 的外接球
的外接球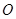 的体积为
的体积为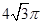 ,则球心
,则球心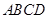 的距离为( )
的距离为( )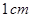 的正方形绕其一条边所在直线旋转一周,则所形成圆柱的体积等于
的正方形绕其一条边所在直线旋转一周,则所形成圆柱的体积等于 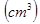 .
.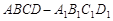 的面对角线
的面对角线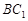 上运动,则下列四个命题:
上运动,则下列四个命题: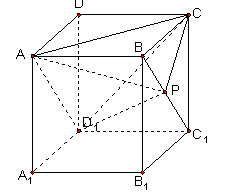
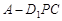 的体积不变;
的体积不变;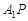 ∥平面
∥平面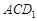 ;
;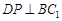 ;
;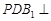 平面
平面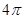 ,底面积为
,底面积为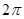 ,则该圆锥的母线长为 .
,则该圆锥的母线长为 . 
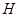 是球
是球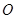 的直径
的直径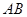 上一点,
上一点,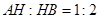 ,
,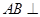 平面
平面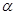 ,
,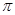 ,则球
,则球