题目内容
(本小题14分) 已知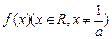 满足ax·f(x)=2bx+f(x), a≠0, f(1)=1且使
满足ax·f(x)=2bx+f(x), a≠0, f(1)=1且使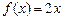 成立的实数x有且只有一个.
成立的实数x有且只有一个.
(1)求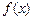 的表达式;
的表达式;
(2)数列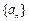 满足:
满足: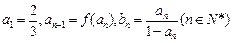 , 证明:
, 证明: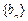 为等比数列.
为等比数列.
(3)在(2)的条件下, 若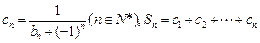 , 求证:
, 求证: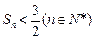
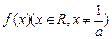 满足ax·f(x)=2bx+f(x), a≠0, f(1)=1且使
满足ax·f(x)=2bx+f(x), a≠0, f(1)=1且使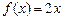 成立的实数x有且只有一个.
成立的实数x有且只有一个.(1)求
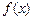 的表达式;
的表达式;(2)数列
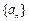 满足:
满足: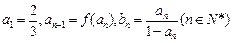 , 证明:
, 证明: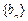 为等比数列.
为等比数列.(3)在(2)的条件下, 若
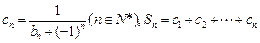 , 求证:
, 求证: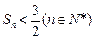
(1)
(2)证明见解析
(3)证明见解析

(2)证明见解析
(3)证明见解析
(1)f(x)= ∴
∴



(2)bn+1=2bn ∴{bn}是首项为2, 公比为2的等比数列;
(3)bn=2n Cn=
C2k+C2k+1= <
<
∴n为奇数时, Sn=C1+(C2+C3)+…+(Cn-1+Cn)<1+
=1+ =
= <
<
n为偶数时, Sn<Sn+1<
综合以上, Sn<
 ∴
∴



(2)bn+1=2bn ∴{bn}是首项为2, 公比为2的等比数列;
(3)bn=2n Cn=

C2k+C2k+1=
 <
<
∴n为奇数时, Sn=C1+(C2+C3)+…+(Cn-1+Cn)<1+

=1+
 =
= <
<
n为偶数时, Sn<Sn+1<

综合以上, Sn<


练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
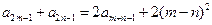
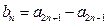 (n∈N*),证明:数列{bn}是等差数列;
(n∈N*),证明:数列{bn}是等差数列;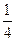
 qn-1(q≠0,n∈N*),求数列{cn}的前n项和Sn.
qn-1(q≠0,n∈N*),求数列{cn}的前n项和Sn.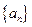 ,
,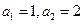 ,对任意
,对任意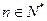 都有
都有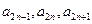 为等比数列,
为等比数列,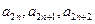 为等差数列
为等差数列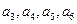 ;
;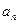 ;
;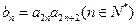 ,求
,求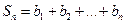 .
.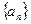 中,
中,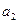 =3,
=3,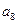 =9,则前9项和
=9,则前9项和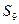 =( )
=( ) 层
层 的六边形点阵.它的中心是一个点,算作第一层, 第2层每边有2个点,第3层每边有3个点 ,…,第
的六边形点阵.它的中心是一个点,算作第一层, 第2层每边有2个点,第3层每边有3个点 ,…,第
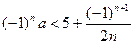 对于任意正整数
对于任意正整数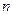 恒成立,则实数
恒成立,则实数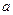 的取值范围是_★_.
的取值范围是_★_.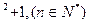 的各位数字之和,如14
的各位数字之和,如14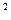 +1=197,1+9+7=17,则f(14)="17." 记f
+1=197,1+9+7=17,则f(14)="17." 记f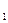 (n)=f(n),f
(n)=f(n),f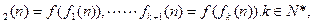 则f
则f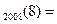
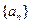 的前
的前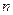 项和为
项和为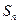 ,若
,若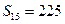 ,则
,则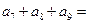 ( ).
( ).  满足
满足 ,其中
,其中 为
为 项和,
项和, ;
; 是等比数列;
是等比数列; 和
和