题目内容
已知数列{an}中,a1= ,点(n,2an+1-an)在直线y=x上,其中n=1,2,3,…
,点(n,2an+1-an)在直线y=x上,其中n=1,2,3,…
(Ⅰ)令bn=an-1-an-1,求证数列{bn}是等比数列;
(Ⅱ)求数列{an}的通项;
(Ⅲ)设Sn、Tn分别为数列{an}、{bn}的前n项和,是否存在实数λ,使得数列 为等差数列?若存在,试求出λ;若不存在,则说明理由。
为等差数列?若存在,试求出λ;若不存在,则说明理由。
 ,点(n,2an+1-an)在直线y=x上,其中n=1,2,3,…
,点(n,2an+1-an)在直线y=x上,其中n=1,2,3,… (Ⅰ)令bn=an-1-an-1,求证数列{bn}是等比数列;
(Ⅱ)求数列{an}的通项;
(Ⅲ)设Sn、Tn分别为数列{an}、{bn}的前n项和,是否存在实数λ,使得数列
 为等差数列?若存在,试求出λ;若不存在,则说明理由。
为等差数列?若存在,试求出λ;若不存在,则说明理由。 解:(Ⅰ)由已知得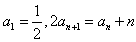 ,
,
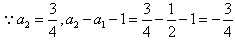 ,
,
又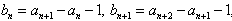 ,
,
∴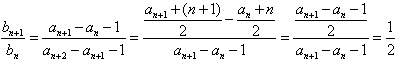 ,
,
∴{bn}是以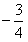 为首项,以
为首项,以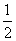 为公比的等比数列;
为公比的等比数列;
(Ⅱ)由(Ⅰ)知,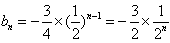 ,
,
∴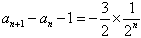 ,
,
∴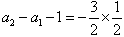 ,
,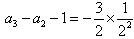 ,……
,……
∴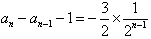 ,
,
将以上各式相加得: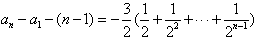 ,
,
∴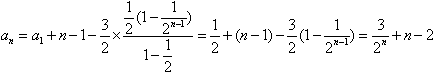 ,
,
∴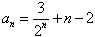 。
。
(Ⅲ)存在λ=2,使数列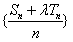 是等差数列,
是等差数列,
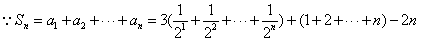
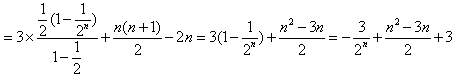 ,
,
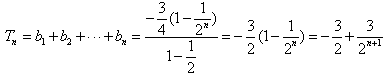 ,
,
数列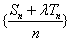 是等差数列的充要条件是
是等差数列的充要条件是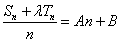 (A、B是常数),
(A、B是常数),
即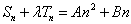 ,
,
又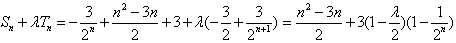 ,
,
∴当且仅当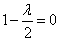 ,即λ=2时,数列
,即λ=2时,数列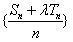 为等差数列。
为等差数列。
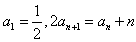 ,
,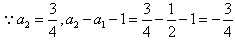 ,
,又
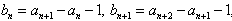 ,
,∴
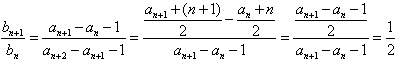 ,
,∴{bn}是以
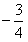 为首项,以
为首项,以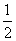 为公比的等比数列;
为公比的等比数列;(Ⅱ)由(Ⅰ)知,
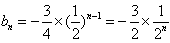 ,
,∴
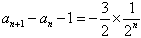 ,
,∴
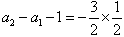 ,
,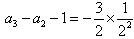 ,……
,…… ∴
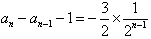 ,
,将以上各式相加得:
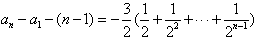 ,
,∴
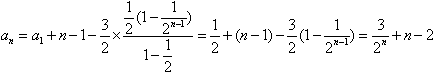 ,
,∴
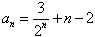 。
。(Ⅲ)存在λ=2,使数列
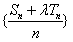 是等差数列,
是等差数列,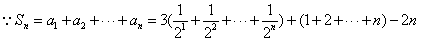
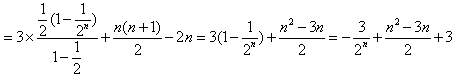 ,
,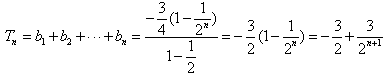 ,
,数列
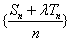 是等差数列的充要条件是
是等差数列的充要条件是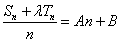 (A、B是常数),
(A、B是常数),即
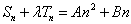 ,
,又
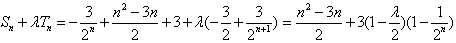 ,
,∴当且仅当
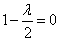 ,即λ=2时,数列
,即λ=2时,数列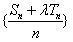 为等差数列。
为等差数列。
练习册系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|