题目内容
某项考试按科目A、科目B依次进行,只有当科目A成绩合格时,才可继续参加科目B的考试.已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证书.现某人参加这项考试,科目A每次考试成绩合格的概率均为 ,科目B每次考试成绩合格的概率均为
,科目B每次考试成绩合格的概率均为 .假设各次考试成绩合格与否均互不影响.
.假设各次考试成绩合格与否均互不影响.(Ⅰ)求他不需要补考就可获得证书的概率;
(Ⅱ)在这项考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为ξ,求p(ξ=3).
【答案】分析:(Ⅰ)根据相互独立事件的概率乘法公式可得他不需要补考就可获得证书的概率.
(Ⅱ)他参加考试的次数为ξ,ξ=3说明他只参加了科目A的补考或只参加了科目B的补考,把只参加科目A补考的概率、只参加科目B的概率相加,即得所求.
解答:解:(Ⅰ)根据相互独立事件的概率乘法公式可得,他不需要补考就可获得证书的概率为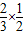 =
= .
.
(Ⅱ)他参加考试的次数为ξ,由题意可得ξ的最大值为4.
ξ=3说明他只参加了科目A的补考或只参加了科目B的补考,
具体是:①科目A补考通过,科目B直接通过;②科目A直接通过,科目B需要补考.
故P(ξ=3)=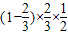 +
+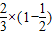 =
= .
.
点评:本题主要考查相互独立事件的概率乘法公式,所求的事件的概率与它的对立事件的概率之间的关系,体现
了分类讨论的数学思想,属于中档题.
(Ⅱ)他参加考试的次数为ξ,ξ=3说明他只参加了科目A的补考或只参加了科目B的补考,把只参加科目A补考的概率、只参加科目B的概率相加,即得所求.
解答:解:(Ⅰ)根据相互独立事件的概率乘法公式可得,他不需要补考就可获得证书的概率为
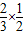 =
= .
.(Ⅱ)他参加考试的次数为ξ,由题意可得ξ的最大值为4.
ξ=3说明他只参加了科目A的补考或只参加了科目B的补考,
具体是:①科目A补考通过,科目B直接通过;②科目A直接通过,科目B需要补考.
故P(ξ=3)=
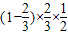 +
+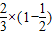 =
= .
.点评:本题主要考查相互独立事件的概率乘法公式,所求的事件的概率与它的对立事件的概率之间的关系,体现
了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目