题目内容
【题目】如图，点
为正方形
的中心，
为正三角形，平面
平面，
是线段
的中点，则（ ）
A.直线
，
是相交直线
B.直线与直线
所成角等于
C.直线
与直线所成角等于直线与直线
所成角
D.直线与平面所成角小于直线平面所成角
【答案】ABD
【解析】
A：结合三角形中位线定理、平行线的性质、梯形的定义进行判断即可；
B：取
的中点为
，利用线面垂直的判定定理、平行线的性质进行判断即可；
C：利用异面直线所成角的定义，计算出直线
与直线
所成角、直线与直线
所成角，然后判断即可；
D：根据线面角的定义求出直线
与平面
所成角和直线
平面所成角，然后比较判断即可.
A：连接
，因为点
为正方形的中心，
是线段
的中点，所以有
，
，因此四边形
是梯形，故直线，是相交直线，所以本选项是正确的；
B：取的中点为
，连接
，
为正三角形，所以有
，点为正方形的中心，所以有
，所以
平面
，因此有
，而
，所以直线与直线所成角等于
，故本选项是正确的；
C：因为，所以
是直线与直线所成角，由正三角形的性质可知，
，因为
，所以
是直线与直线所成角.连接
，设正方形的边长为2，由勾股定理以及上述的分析可知：
，所以
，因此有
，由余弦定理可知：
，所以本选项是错误的；
D：取
的中点
，连接
，所以
平面，所以
是直线与平面所成角，
，所以
，
是直线平面所成角，
，因为
，所以直线与平面所成角小于直线平面所成角，故本选项是正确的.
故选：ABD
【题目】某学校为了了解初三学生的体育锻炼情况，随机抽取了40名学生对一周的体育锻炼时间长（单位：小时）进行统计，并将数据整理如下：
时间长 性别 |
|
|
|
|
|
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
（1）采用样本估计总体的方式，试估计该校的所有学生中一周的体育锻炼时间长为
的概率；
（2）若将一周的体育锻炼时间长不低于3小时的评定为“体育锻炼合格者”，否则为“不合格者”，根据以上数据完成下面的
列联表，并据此判断能否有95%的把握认为体育锻炼与性别有关？附：
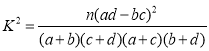，其中
.
| 0.10 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
