题目内容
【题目】在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,抛物线
,抛物线![]() 的方程为
的方程为![]() ,过
,过![]() 作动直线
作动直线![]() 交抛物线于
交抛物线于![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() .
.
(1)若![]() 与
与![]() 重合,求直线
重合,求直线![]() 的方程;
的方程;
(2)求直线![]() 的斜率的取值范围.
的斜率的取值范围.
【答案】(1) ![]() ; (2)
; (2) ![]()
【解析】
(1)由已知利用“点差法”求得直线斜率,代入直线方程点斜式得答案;
(2)当直线斜率不存在时,求得![]() 的坐标,可得
的坐标,可得![]() 的斜率,当直线的斜率存在时,设出直线方程,与抛物线方程联立,利用根与系数的关系求得
的斜率,当直线的斜率存在时,设出直线方程,与抛物线方程联立,利用根与系数的关系求得![]() 的坐标,可得
的坐标,可得![]() 所在直线斜率,然后利用基本不等式求最值.
所在直线斜率,然后利用基本不等式求最值.
(1)设![]() ,如图
,如图
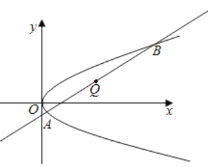
![]() 与
与![]() 重合,即
重合,即![]() 为
为![]() 中点.则
中点.则![]() ,
,
则有![]() ,
,
两式相减得![]() ,
,
即![]()
![]()
所以直线![]() 的方程为:
的方程为:![]() ,即
,即![]() .
.
(2)当直线![]() 轴时,
轴时,![]() ,
,![]() 的斜率为0;
的斜率为0;
当直线![]() 的斜率存在且不为0时,设直线
的斜率存在且不为0时,设直线![]() 的方程为
的方程为
联立![]() ,得
,得![]() .
.
则![]() ,
,![]() .
.
所以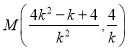
所以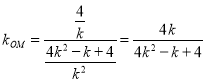
当![]() 时,
时, 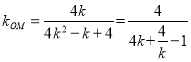
由![]() 当且仅当
当且仅当![]() 时取等号.
时取等号.
所以此时![]() ,
,
当![]() 时,
时, 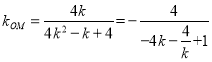
同理可得此时![]()
所以直线![]() 的斜率的取值范围是
的斜率的取值范围是![]() .
.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目