题目内容
数列{an}满足a1=1,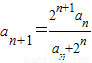 (n∈N+).
(n∈N+).(Ⅰ)证明:数列
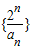 是等差数列;
是等差数列;(Ⅱ)求数列{an}的通项公式an;
(Ⅲ)设bn=n(n+1)an,求数列{bn}的前n项和Sn.
【答案】分析:(I)由已知中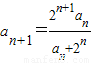 (n∈N+),我们易变形得:
(n∈N+),我们易变形得: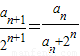 ,即
,即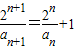 ,进而根据等差数列的定义,即可得到结论;
,进而根据等差数列的定义,即可得到结论;
(II)由(I)的结论,我们可以先求出数列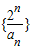 的通项公式,进一步得到数列{an}的通项公式an;
的通项公式,进一步得到数列{an}的通项公式an;
(Ⅲ)由(II)中数列{an}的通项公式,及bn=n(n+1)an,我们易得到数列{bn}的通项公式,由于其通项公式由一个等差数列与一个等比数列相乘得到,故利用错位相消法,即可求出数列{bn}的前n项和Sn.
解答:解:(Ⅰ)证明:由已知可得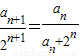 ,
,
即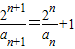 ,
,
即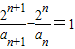
∴数列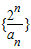 是公差为1的等差数列(5分)
是公差为1的等差数列(5分)
(Ⅱ)由(Ⅰ)知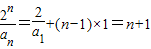 ,
,
∴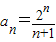 (8分)
(8分)
(Ⅲ)由(Ⅱ)知bn=n•2n
Sn=1•2+2•22+3•23++n•2n
2Sn=1•22+2•23+…+(n-1)•2n+n•2n+1(10分)
相减得: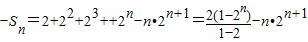 =2n+1-2-n•2n+1(12分)
=2n+1-2-n•2n+1(12分)
∴Sn=(n-1)•2n+1+2
点评:本题考查的知识点是数列的递推公式及数列求各,其中(I)中利用递推公式,得到数列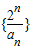 是等差数列并求出其通项公式是解答本题的关键.
是等差数列并求出其通项公式是解答本题的关键.
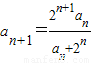 (n∈N+),我们易变形得:
(n∈N+),我们易变形得: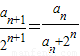 ,即
,即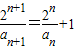 ,进而根据等差数列的定义,即可得到结论;
,进而根据等差数列的定义,即可得到结论;(II)由(I)的结论,我们可以先求出数列
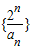 的通项公式,进一步得到数列{an}的通项公式an;
的通项公式,进一步得到数列{an}的通项公式an;(Ⅲ)由(II)中数列{an}的通项公式,及bn=n(n+1)an,我们易得到数列{bn}的通项公式,由于其通项公式由一个等差数列与一个等比数列相乘得到,故利用错位相消法,即可求出数列{bn}的前n项和Sn.
解答:解:(Ⅰ)证明:由已知可得
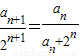 ,
,即
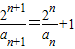 ,
,即
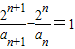
∴数列
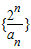 是公差为1的等差数列(5分)
是公差为1的等差数列(5分)(Ⅱ)由(Ⅰ)知
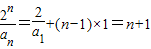 ,
,∴
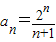 (8分)
(8分)(Ⅲ)由(Ⅱ)知bn=n•2n
Sn=1•2+2•22+3•23++n•2n
2Sn=1•22+2•23+…+(n-1)•2n+n•2n+1(10分)
相减得:
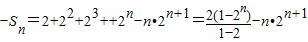 =2n+1-2-n•2n+1(12分)
=2n+1-2-n•2n+1(12分)∴Sn=(n-1)•2n+1+2
点评:本题考查的知识点是数列的递推公式及数列求各,其中(I)中利用递推公式,得到数列
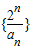 是等差数列并求出其通项公式是解答本题的关键.
是等差数列并求出其通项公式是解答本题的关键. 
练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目