题目内容
设函数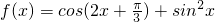
(Ⅰ)求函数f(x)的最大值和最小正周期;
(Ⅱ)设A,B,C为△ABC的三个内角,若cosB= ,f(
,f( )=-
)=- ,求sinA.
,求sinA.
解:(Ⅰ)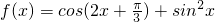 =
= +
+ =
= ,
,
故函数f(x)的最大值为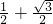 ,最小正周期 T=
,最小正周期 T= =π.
=π.
(Ⅱ)f( )=
)= =-
=- ,∴sinC=
,∴sinC= ,又C为锐角,故C=
,又C为锐角,故C= .
.
∵cosB= ,∴sinB=
,∴sinB= .∴sinA=sin(B+C)=sinBcosC+cosBsinC=
.∴sinA=sin(B+C)=sinBcosC+cosBsinC= .
.
分析:(Ⅰ)利用两角和的余弦公式化简函数f(x)为 ,可得最大值为
,可得最大值为 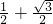 ,最小正周期 T=
,最小正周期 T= .
.
(Ⅱ)由f( )=-
)=- 求得C=
求得C= ,由cosB=
,由cosB= 求得 sinB,利用sinA=sin(B+C)=sinBcosC+cosBsinC 求出结果.
求得 sinB,利用sinA=sin(B+C)=sinBcosC+cosBsinC 求出结果.
点评:本题考查两角和的余弦公式、正弦公式的应用,求出角C是解题的关键.
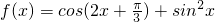 =
= +
+ =
= ,
,故函数f(x)的最大值为
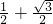 ,最小正周期 T=
,最小正周期 T= =π.
=π. (Ⅱ)f(
 )=
)= =-
=- ,∴sinC=
,∴sinC= ,又C为锐角,故C=
,又C为锐角,故C= .
.∵cosB=
 ,∴sinB=
,∴sinB= .∴sinA=sin(B+C)=sinBcosC+cosBsinC=
.∴sinA=sin(B+C)=sinBcosC+cosBsinC= .
.分析:(Ⅰ)利用两角和的余弦公式化简函数f(x)为
 ,可得最大值为
,可得最大值为 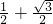 ,最小正周期 T=
,最小正周期 T= .
.(Ⅱ)由f(
 )=-
)=- 求得C=
求得C= ,由cosB=
,由cosB= 求得 sinB,利用sinA=sin(B+C)=sinBcosC+cosBsinC 求出结果.
求得 sinB,利用sinA=sin(B+C)=sinBcosC+cosBsinC 求出结果.点评:本题考查两角和的余弦公式、正弦公式的应用,求出角C是解题的关键.

练习册系列答案
相关题目
 设函数
设函数