题目内容
6.已知函数f(x)的定义域为(0,4),函数g(x)=$\frac{{f({x+1})}}{{\sqrt{x-1}}}$的定义域为集合A,集合B={x|a<x<2a-1},若A∩B=B,求实数a的取值范围.分析 根据f(x)的定义域便可得出函数g(x)的自变量x满足$\left\{\begin{array}{l}{0<x+1<4}\\{x-1>0}\end{array}\right.$,从而得出集合A={x|1<x<3},而由A∩B=B便知B⊆A,这样可看出:讨论B=∅和B≠∅两种情况,求出每种情况的a的范围,再求并集便可得出实数a的取值范围.
解答 解:要使g(x)有意义,则:$\left\{\begin{array}{l}{0<x+1<4}\\{x>1}\end{array}\right.$;
∴1<x<3;
∴A={x|1<x<3};
∵A∩B=B;
∴B⊆A;
①若B=∅,满足B⊆A,则a≥2a-1;
∴a≤1;
②若B≠∅,则:$\left\{\begin{array}{l}{a≥1}\\{2a-1≤3}\\{a<2a-1}\end{array}\right.$;
∴1<a≤2;
∴a≤2;
∴实数a的取值范围为(-∞,2].
点评 考查描述法表示集合,函数定义域的概念及其求法,空集的概念,交集、子集的概念,不要漏了B=∅的情况.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
16.下列函数中,在区间(0,+∞)上是增函数的是( )
| A. | y=-x2+1 | B. | y=-2x+3 | C. | y=log3x | D. | $y={(\frac{1}{2})^x}$ |
17.函数y=x2-2x-1,x∈[0,3]的值域为( )
| A. | [-1,2] | B. | [-2,2] | C. | [-2,-1] | D. | [-1,1] |
1.已知函数f(x+1)=3x+1,则f(x)的解析式为( )
| A. | f(x)=3-2x | B. | f(x)=2-3x | C. | f(x)=3x-2 | D. | f(x)=3x |
11.已知$\overrightarrow{a}=(1,x)$和$\overrightarrow{b}=(x+2,-2)$,若$\overrightarrow{a}⊥\overrightarrow{b}$,则|$\overrightarrow{a}+\overrightarrow{b}$|=( )
| A. | 5 | B. | 8 | C. | $\sqrt{10}$ | D. | 64 |
18.已知点A(1,2),B(4,3),向量$\overrightarrow{AC}=({-2,-2})$,则向量$\overrightarrow{BC}$=( )
| A. | (-5,-3) | B. | (5,3) | C. | (1,-1) | D. | (-1,-1) |
15.下列函数中为偶函数的是( )
| A. | y=$\frac{1}{x}$ | B. | y=lg|x| | C. | y=(x-1)2 | D. | y=2x |
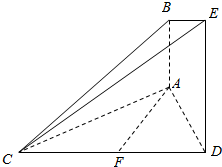 如图所示,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2a,F为CD的中点.
如图所示,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2a,F为CD的中点.