Question

求抛物线y²=64x上的点到直线4x+3y+46=0的距离的最小值,并求取得最小值时的抛物线上的点的坐标.

Answer 1

解法一:设P(x₀,y₀)是抛物线上的点,则y₀²=64x₀,

∴d==|4·+3y₀+46|=［(y₀+24)²+160］.

∴当y₀=-24,x₀=9时,d有最小值2.

此时抛物线上点的坐标为(9,-24).

解法二:由无实根,知直线与抛物线没有公共点.

设与直线4x+3y+46=0平行的直线为y=－x+b,代入y²=64x得y²+48y－48b=0.①

设此直线与抛物线相切,即只有一个公共点.

∴Δ=48²－4(－48b)=0.解得b=－12.代入①,

得y=－24,x=9,即点P(9,－24)到直线4x+3y+46=0的距离最近,最近距离d=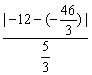=2.