题目内容
下列各组函数是同一函数的是
①f(x)= 与g(x)=x
与g(x)=x ,
,
②f(x)=|x| ,
,
③f(x)=
 与g(x)=
与g(x)=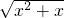 ,
,
④f(x)=x2-2x-1与g(t)=t2-2t-1.
- A.①③
- B.②③
- C.②④
- D.①④
C
分析:两个函数是同一函数,必须同时满足两个条件:①定义域相同;②对应法则相同.
解答:①由于f(x)= 与g(x)=x
与g(x)=x 的定义域是{x|x≤0},且f(x)=
的定义域是{x|x≤0},且f(x)= =|x|
=|x| ≠g(x)
≠g(x)
∴f(x)= 与g(x)=x
与g(x)=x 不是同一函数,故①不正确;
不是同一函数,故①不正确;
②∵f(x)=|x|与g(x)= 的定义域都是R,且g(x)=
的定义域都是R,且g(x)= =|x|=f(x),
=|x|=f(x),
∴f(x)=|x|与g(x)= 是同一函数,故②正确;
是同一函数,故②正确;
③∵f(x)= 的定义域是{x|x>0},g(x)=
的定义域是{x|x>0},g(x)=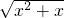 的定义域都是{x|x>0或x<-1},
的定义域都是{x|x>0或x<-1},
∴f(x)=
 与g(x)=
与g(x)=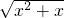 不是同一函数,故③不正确;
不是同一函数,故③不正确;
④∵f(x)=x2-2x-1与g(t)=t2-2t-1定义域都是R,且对应法则相同
∴f(x)=x2-2x-1与g(t)=t2-2t-1是同一函数,故④正确.
故答案为 C.
点评:本题考查同一函数的判断与应用,是基础题.解题时要认真审题,仔细解答.
分析:两个函数是同一函数,必须同时满足两个条件:①定义域相同;②对应法则相同.
解答:①由于f(x)=
 与g(x)=x
与g(x)=x 的定义域是{x|x≤0},且f(x)=
的定义域是{x|x≤0},且f(x)= =|x|
=|x| ≠g(x)
≠g(x)∴f(x)=
 与g(x)=x
与g(x)=x 不是同一函数,故①不正确;
不是同一函数,故①不正确;②∵f(x)=|x|与g(x)=
 的定义域都是R,且g(x)=
的定义域都是R,且g(x)= =|x|=f(x),
=|x|=f(x),∴f(x)=|x|与g(x)=
 是同一函数,故②正确;
是同一函数,故②正确;③∵f(x)=
 的定义域是{x|x>0},g(x)=
的定义域是{x|x>0},g(x)=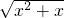 的定义域都是{x|x>0或x<-1},
的定义域都是{x|x>0或x<-1},∴f(x)=

 与g(x)=
与g(x)=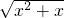 不是同一函数,故③不正确;
不是同一函数,故③不正确;④∵f(x)=x2-2x-1与g(t)=t2-2t-1定义域都是R,且对应法则相同
∴f(x)=x2-2x-1与g(t)=t2-2t-1是同一函数,故④正确.
故答案为 C.
点评:本题考查同一函数的判断与应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目




