题目内容
已知a,b,c为△ABC的三个内角A,B,C的对边,向量m=( ,-1),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角A,B的大小分别为( )
,-1),n=(cosA,sinA).若m⊥n,且acosB+bcosA=csinC,则角A,B的大小分别为( )
(A) ,
, (B)
(B) ,
,
(C) ,
, (D)
(D) ,
,
C
解析

练习册系列答案
相关题目
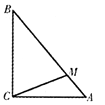
如图,△ABC中,∠C =90°,且AC=BC=4,点M满足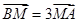 ,则
,则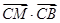 =( )
=( )
| A.2 | B.3 | C.4 | D.6 |
已知向量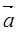 =(2,t),
=(2,t),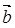 =(1,2),若t=t1时,
=(1,2),若t=t1时,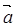 ∥
∥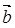 ;t=t2时,
;t=t2时,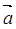 ⊥
⊥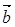 ,则( )
,则( )
| A.t1=-4,t2=-1 | B.t1=-4,t2=1 | C.t1=4,t2=-1 | D.t1=4, t2=1 |
定义: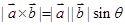 ,其中
,其中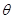 为向量
为向量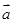 与
与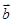 的夹角,若
的夹角,若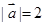 ,
,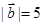 ,
,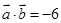 ,则
,则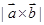 等于( )
等于( )
A. | B.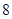 | C. 或 或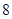 | D.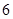 |
下列说法中:⑴若向量 ,则存在实数
,则存在实数 ,使得
,使得 ;
;
⑵非零向量 ,若满足
,若满足 ,则
,则
⑶与向量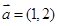 ,
, 夹角相等的单位向量
夹角相等的单位向量
⑷已知 ,若对任意
,若对任意 ,
,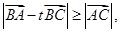 则
则 一定为锐角三角形。
一定为锐角三角形。
其中正确说法的序号是( )
| A.(1)(2) | B.(1)(3) | C.(2)(4) | D.(2) |
若向量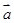 与
与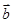 的夹角为120°,且
的夹角为120°,且 ,则有( )
,则有( )
A.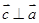 | B.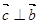 | C.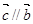 | D.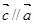 |
若a=(2,3),b=(-4,7),则a在b方向上的投影为( )
A. |
B. |
C. |
D. |
在△ABC中,AB=2,AC=3,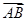 ·
·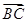 =1,则BC=( ).
=1,则BC=( ).
A.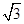 | B. | C.2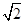 | D.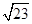 |
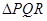 是圆O的内接正三角形,当
是圆O的内接正三角形,当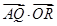 的取值范围是( )
的取值范围是( )