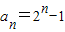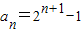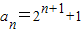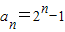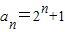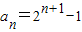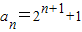Question

已知{a_n}满足：

12

a1

+

22

a2

+

32

a3

+…+

n2

an

=(

n(n+1)

2

)2 （n=1，2，3，…）．
（Ⅰ） 求{a_n}的通项公式；
（Ⅱ） 若数列{b_n}满足，bn=

a 2n

2an+1

（n=1，2，3，…），试{b_n}前n项的和S_n．

Answer 1

（Ⅰ）由

12

a1

+

22

a2

+…+

n2

an

=(

n(n+1)

2

)2①
当n≥2时，

12

a1

+

22

a2

+…+

(n-1)2

an-1

=(

n(n-1)

2

)2②
①-②得：

n2

an

=

n(n+1)+n(n-1)

2

×

n(n+1)-n(n-1)

2

=n³，
所以，an=

1

n

（n≥2）．
当n=1时，a₁=1符合an=

1

n

，所以，an=

1

n

；
（Ⅱ）由bn=

an2

2an+1

=

1 n2

2 n +1

=

1

n(n+2)

．
所以，S_n=b₁+b₂+…+b_n
=

1

2

(1-

1

3

+

1

2

-

1

4

+

1

3

-

1

5

+…+

1

n-1

-

1

n+1

+

1

n

-

1

n+2

)
=

1

2

(1+

1

2

-

1

n+1

-

1

n+2

)
=

3

4

-

2n+3

2(n+1)(n+2)

．