题目内容
已知双曲线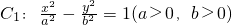 的离心率为2,若抛物线
的离心率为2,若抛物线 的焦点到双曲线C1的渐近线的距离为2,若A、B是C2上两点且OA⊥OB,则直线AB与y轴的交点的纵坐标为
的焦点到双曲线C1的渐近线的距离为2,若A、B是C2上两点且OA⊥OB,则直线AB与y轴的交点的纵坐标为
- A.

- B.16
- C.8
- D.
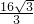
B
分析:抛物线焦点为F(0, ),由e=
),由e= =2,抛物线焦点至双曲线一渐近线距离d=
=2,抛物线焦点至双曲线一渐近线距离d= =2,推导出抛物线方程为:x2=±16y,设A(x1,y1),B(x2,y2),由
=2,推导出抛物线方程为:x2=±16y,设A(x1,y1),B(x2,y2),由 ,得到x1x2=-256,y1y2=256.设AB方程为:y=kx+m,根据韦达定理,x1x2=-16m,从而得到m=16,由此能求出直线AB与y轴的交点的纵坐标.
,得到x1x2=-256,y1y2=256.设AB方程为:y=kx+m,根据韦达定理,x1x2=-16m,从而得到m=16,由此能求出直线AB与y轴的交点的纵坐标.
解答:抛物线焦点为F(0, ),
),
e= =2,
=2,
∴c=2a,
b= =
= ,
,
双曲线一渐近线方程为:y=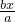 =
= ,
,
 =0,
=0,
∵抛物线焦点至双曲线一渐近线距离d= =2,
=2,
∴p=±8,
∴抛物线方程为:x2=±16y,
设A(x1,y1),B(x2,y2),
∴ =(x1,y1),
=(x1,y1), =(x
=(x ,y2),
,y2),
∵ ,∴
,∴ •
• =0.
=0.
∴x1x2+y1y2=0,
∵ =16y1,
=16y1, =16y2,
=16y2,
∴x1x2+ =0,
=0,
∴x1x2=-256,①
y1y2=256,②
设AB方程为:y=kx+m,
x2=±16(kx+m),
x2±16kx-16m=0,
根据韦达定理,x1x2=-16m,
由①式得:-256=-16m,
∴m=16,
由直线方程x=kx+m可知,m是直线在y轴的截距,即是交点的纵坐标,
∴直线AB与y轴的交点的纵坐标为16,
故选B.
点评:本题考查直线与y轴交点的纵坐标的求法,具体涉及到双曲线、抛物线、韦达定理、点到直线的距离公式等基本知识点,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.
分析:抛物线焦点为F(0,
 ),由e=
),由e= =2,抛物线焦点至双曲线一渐近线距离d=
=2,抛物线焦点至双曲线一渐近线距离d= =2,推导出抛物线方程为:x2=±16y,设A(x1,y1),B(x2,y2),由
=2,推导出抛物线方程为:x2=±16y,设A(x1,y1),B(x2,y2),由 ,得到x1x2=-256,y1y2=256.设AB方程为:y=kx+m,根据韦达定理,x1x2=-16m,从而得到m=16,由此能求出直线AB与y轴的交点的纵坐标.
,得到x1x2=-256,y1y2=256.设AB方程为:y=kx+m,根据韦达定理,x1x2=-16m,从而得到m=16,由此能求出直线AB与y轴的交点的纵坐标.解答:抛物线焦点为F(0,
 ),
),e=
 =2,
=2,∴c=2a,
b=
 =
= ,
,双曲线一渐近线方程为:y=
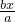 =
= ,
, =0,
=0,∵抛物线焦点至双曲线一渐近线距离d=
 =2,
=2,∴p=±8,
∴抛物线方程为:x2=±16y,
设A(x1,y1),B(x2,y2),
∴
 =(x1,y1),
=(x1,y1), =(x
=(x ,y2),
,y2),∵
 ,∴
,∴ •
• =0.
=0.∴x1x2+y1y2=0,
∵
 =16y1,
=16y1, =16y2,
=16y2,∴x1x2+
 =0,
=0,∴x1x2=-256,①
y1y2=256,②
设AB方程为:y=kx+m,
x2=±16(kx+m),
x2±16kx-16m=0,
根据韦达定理,x1x2=-16m,
由①式得:-256=-16m,
∴m=16,
由直线方程x=kx+m可知,m是直线在y轴的截距,即是交点的纵坐标,
∴直线AB与y轴的交点的纵坐标为16,
故选B.
点评:本题考查直线与y轴交点的纵坐标的求法,具体涉及到双曲线、抛物线、韦达定理、点到直线的距离公式等基本知识点,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
相关题目
已知双曲线的离心率为2,焦点是(-4,0),(4,0),则双曲线方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 的离心率为2,焦点到渐近线的距离等于
的离心率为2,焦点到渐近线的距离等于 ,过右焦点
,过右焦点 的直线
的直线
 、
、 两点,
两点, 为左焦点,
为左焦点, 的面积等于
的面积等于 ,求直线
,求直线 的方程.
的方程. 的离心率为2,焦点到渐近线的距离为
的离心率为2,焦点到渐近线的距离为 ,点P的坐标为(0,-2),过P的直线l与双曲线C交于不同两点M、N.
,点P的坐标为(0,-2),过P的直线l与双曲线C交于不同两点M、N.
 (O为坐标原点),求t的取值范围
(O为坐标原点),求t的取值范围