题目内容
【题目】（12分）已知椭圆C：
（a>b>0），四点P1（1,1），P2（0,1），P3（–1，
），P4（1，）中恰有三点在椭圆C上.
（1）求C的方程；
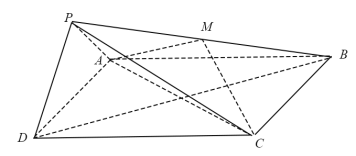
（2）设直线l不经过P2点且与C相交于A，B两点.若直线P2A与直线P2B的斜率的和为–1，证明：l过定点.
【答案】（1）C的方程为
（2）详见解析
【解析】（1）由于
，
两点关于y轴对称，故由题设知C经过，两点.
又由
知，C不经过点P1，所以点P2在C上.
因此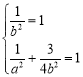
，解得
.
故C的方程为.
（2）设直线P2A与直线P2B的斜率分别为k1，k2，
如果l与x轴垂直，设l：x=t，由题设知
，且
，可得A，B的坐标分别为（t，
），（t，
）.
则
，得
，不符合题设.
从而可设l：
（
）.将代入得
由题设可知
.
设A（x1，y1），B（x2，y2），则x1+x2=
，x1x2=
.
而
.
由题设
，故
.
即
.
解得
.
当且仅当
时，
，欲使l：
，即
，
所以l过定点（2，
）
练习册系列答案
相关题目
【题目】在物理实验中，为了研究所挂物体的重量x对弹簧长度y的影响．某学生通过实验测量得到物体的重量与弹簧长度的对比表：
物体重量（单位g） | 1 | 2 | 3 | 4 | 5 |
弹簧长度（单位cm） | 1.5 | 3 | 4 | 5 | 6.5 |
参考公式：
①．样本数据x1 ， x2 ， …xn的标准差
s= 
，其中 
为样本的平均数；
②．线性回归方程系数公式 
= 
= 
， 
= 
﹣ ．
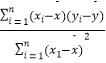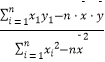（1）画出散点图；
（2）利用所给的参考公式，求y对x的回归直线方程；
（3）预测所挂物体重量为8g时的弹簧长度．
