题目内容
在△ABC中,内角A、B、C对边分别是已知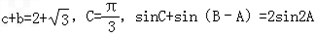 ,求△ABC的面积.
,求△ABC的面积.
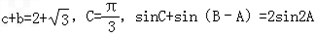 ,求△ABC的面积.
,求△ABC的面积.解:由题意得:sin(B+A)+sin(B﹣A)=4sinAcosA,即sinBcosA=2sinAcosA,
当cosA=0时,则A= ,B=
,B=  ,则a=2b,c=
,则a=2b,c=  b,
b,
又c+b=2+ ,所以b=
,所以b= ,c=
,c=  ,
,
所以S△ABC= bcsinA=
bcsinA=  ;
;
当cosA≠0时,得sinB=2sinA,
由正弦定理得:b=2a,①
又由余弦定理得:cos =
=  =
= ,②
,②
将①代入②,解得a=1或a=7+4 >b+c=2+
>b+c=2+  (舍去),
(舍去),
b=2,此时c= ,
,
所以△ABC是直角三角形,所以S△ABC= ac=
ac=  ,
,
综上,△ABC的面积为 或
或 .
.
当cosA=0时,则A=
 ,B=
,B=  ,则a=2b,c=
,则a=2b,c=  b,
b,又c+b=2+
 ,所以b=
,所以b= ,c=
,c=  ,
,所以S△ABC=
 bcsinA=
bcsinA=  ;
;当cosA≠0时,得sinB=2sinA,
由正弦定理得:b=2a,①
又由余弦定理得:cos
 =
=  =
= ,②
,② 将①代入②,解得a=1或a=7+4
 >b+c=2+
>b+c=2+  (舍去),
(舍去),b=2,此时c=
 ,
,所以△ABC是直角三角形,所以S△ABC=
 ac=
ac=  ,
,综上,△ABC的面积为
 或
或 .
. 
练习册系列答案
相关题目