题目内容
已知空间直角坐标系0-xyz中的动点P（x，y，z）满足：x+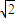
y+z=1，则|OP|的最小值等于 ．
【答案】分析：根据题意，动点P与原点在平面x+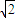
y+z=1内的射影重合时，|OP|取得最小值．再求经过原点与平面x+
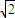y+z=1垂直的直线与平面x+
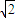y+z=1的交点Q，利用距离公式求出OQ的长，即可得到|OP|取得最小值．
解答：解：∵P（x，y，z）是平面x+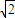
y+z=1内的点，
∴点P与原点在平面x+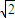
y+z=1内的射影重合时，|OP|取得最小值
过原点与平面x+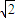
y+z=1垂直的直线方向向量为
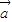=（1，
，1）
∴过原点与平面x+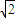
y+z=1垂直的直线方程为：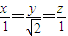
直线方程与平面方程联解，得原点在平面x+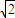
y+z=1内的射影点为Q（
，
，
）
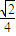∵|OQ|=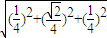
=
∴动点P与Q重合时，|OP|取得最小值为
故答案为：
点评：本题给出平面上动点，求该点到原点距离的最小值，着重考查了空间两点的距离和平面垂线的求法等知识，属于基础题．
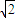y+z=1内的射影重合时，|OP|取得最小值．再求经过原点与平面x+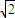y+z=1垂直的直线与平面x+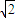y+z=1的交点Q，利用距离公式求出OQ的长，即可得到|OP|取得最小值．解答：解：∵P（x，y，z）是平面x+
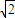y+z=1内的点，∴点P与原点在平面x+
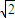y+z=1内的射影重合时，|OP|取得最小值过原点与平面x+
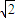y+z=1垂直的直线方向向量为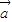=（1，，1）∴过原点与平面x+
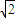y+z=1垂直的直线方程为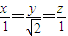：直线方程与平面方程联解，得原点在平面x+
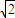y+z=1内的射影点为Q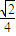（，，）∵|OQ|=
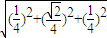=∴动点P与Q重合时，|OP|取得最小值为
故答案为：
点评：本题给出平面上动点，求该点到原点距离的最小值，着重考查了空间两点的距离和平面垂线的求法等知识，属于基础题．
练习册系列答案
相关题目