题目内容
已知椭圆![]() ,
,![]() 为其右焦点,离心率为
为其右焦点,离心率为![]() .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点![]() ,问是否存在直线
,问是否存在直线![]() ,使
,使![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() .若存在,求出
.若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【命题意图】本题考查圆与椭圆的方程等相关知识,考查运算求解能力以及分析问题、解决问题的能力.较难题.
解:(Ⅰ)由题意知:![]() ,∵离心率
,∵离心率![]() ,∴
,∴![]() ,
,![]() ,故所求椭圆C的标准方程为
,故所求椭圆C的标准方程为![]() . ………………………………………………………………………………4分
. ………………………………………………………………………………4分
(Ⅱ)假设存在这样的直线![]()
![]() 满足题意,设
满足题意,设![]() ,
,![]() 的中点为
的中点为![]() .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]() .…………………………5分
.…………………………5分
由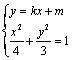 ,得
,得![]() .根据题意,
.根据题意,![]() ,得
,得![]() .且
.且![]() ,所以
,所以![]() ,
,![]() .………8分
.………8分
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴![]() ,∴
,∴![]() .
.
解得![]() ,或
,或![]() .………………………………………………………………10分
.………………………………………………………………10分
当![]() 时,
时,![]() (
(![]() ),显然符合题意;当
),显然符合题意;当![]() 时,代入
时,代入![]() ,得
,得![]() ,解得
,解得![]() .
.
综上所述,存在这样的直线![]() ,其斜率
,其斜率![]() 的取值范围是
的取值范围是![]()

练习册系列答案
相关题目

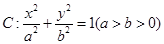 的左、右焦点分别为
的左、右焦点分别为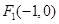 、
、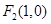 ,P为椭圆
,P为椭圆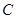 上任意一点,且
上任意一点,且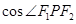 的最小值为
的最小值为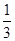 .
.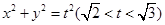 与椭圆
与椭圆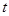 为何值时,矩形ABCD的面积取得最大值?并求出其最大面积.
为何值时,矩形ABCD的面积取得最大值?并求出其最大面积.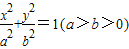 的左、右焦点分别为F1,F2,其右准线l与x轴的交点为T,过椭圆的上顶点A作椭圆的右准线l的垂线,垂足为D,四边形AF1F2D为平行四边形.
的左、右焦点分别为F1,F2,其右准线l与x轴的交点为T,过椭圆的上顶点A作椭圆的右准线l的垂线,垂足为D,四边形AF1F2D为平行四边形.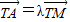 ?若存在,求出实数λ的值;若不存在,请说明理由;
?若存在,求出实数λ的值;若不存在,请说明理由;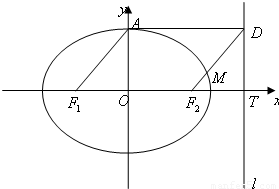
 的左、右焦点分别为F1,F2,其右准线上l上存在点A(点A在x轴上方),使△AF1F2为等腰三角形.
的左、右焦点分别为F1,F2,其右准线上l上存在点A(点A在x轴上方),使△AF1F2为等腰三角形. 到两焦点F1,F2的距离之和为
到两焦点F1,F2的距离之和为 ,求△AF1F2的内切圆的方程.
,求△AF1F2的内切圆的方程.