Question

如图，在棱长为1的正方体ABCD—A₁B₁C₁D₁中，AC与BD交于点E，BC₁与B₁C交于点F.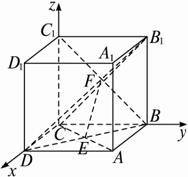

（1）求证：A₁C⊥平面BDC₁；

（2）求二面角B-EF-C的大小（结果用反三角函数值表示）.

Answer 1

思路分析：对于和正方体相关的问题，通常可以考虑建立直角坐标系解决.要证明线面垂直，根据线面垂直的判定定理，证明直线与这个面内的两条相交直线垂直，利用向量的数量积知识，

    转而证明相应的向量的数量积为零即可；要求二面角的大小，可以考虑先求对应的二面角的两个面的法向量的夹角，由此求得对应的二面角的大小.

（1）证明:以点C为坐标原点建立如图所示的空间直角坐标系,则C（0，0，0），

D（1，0，0），B（0，1，0），A₁（1，1，1），C₁（0，0，1），D₁（1，0，1）.

∴=（1，1，1），=（1，-1，0），=（-1，0，1），·=-1+1=0.

∴·=1-1=0，即CA₁⊥DC₁,CA₁⊥BD.又BD∩DC₁=D，

∴A₁C⊥平面BDC₁.

（2）解：同（1）可证，BD₁⊥平面AB₁C，

〈，〉就是所求的二面角的平面角的补角.

∵=（-1，-1，-1），=（-1，1，-1），

∴cos〈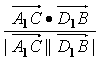，〉==.故二面角B-EF-C的大小是π-arccos.

方法归纳 对于有关立体几何问题，如果有方便建立空间直角坐标系的条件（主要是指当题目的条件中出现了一个点处有三条两两垂直的直线）时，通常在处理相关问题的过程中可以考虑建立坐标系，从而借助于向量的有关知识将问题解决.