题目内容
 如图,已知三棱锥
如图,已知三棱锥![]() 的侧棱
的侧棱![]() 两两垂直,且
两两垂直,且![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)求![]() 点到面
点到面![]() 的距离;
的距离;
(2)求异面直线![]() 与
与![]() 所成的角;
所成的角;
(3)求二面角![]() 的大小.
的大小.
解:(1)取BC的中点D,连AD、OD
因为OB=OC,则OD^BC、AD^BC,BC^面OAD.
过O点作OH^AD于H,则OH^面ABC,OH的长就
是所求的距离. 又BC=2![]() ,OD=
,OD=![]()
=![]() ,又OA^OB,OA^OC OA^面OBC,则OA^OD
,又OA^OB,OA^OC OA^面OBC,则OA^OD
AD=![]() ,在直角三角形OAD中,
,在直角三角形OAD中,

有OH=![]()
(另解:由等体积变换法也可求得答案)
(2)取OA的中点M,连EM、BM,则
EM//AC,ÐBEM是异面直线BE与AC
所成的角,易求得EM=![]() ,BE=
,BE=![]() ,
,
BM=![]() .由余弦定理可求得cosÐBEM=
.由余弦定理可求得cosÐBEM=![]() ,
,
ÐBEM=arccos![]()
(3)连CM并延长交AB于F,连OF、EF.
由OC^面OAB,得OC^AB,又OH^面ABC,所以CF^AB,EF^AB,则ÐEFC就是所求的二面角的平面角.
作EG^CF于G,则EG=![]() OH=
OH=![]() ,在Rt△OAB中,OF=
,在Rt△OAB中,OF=![]()
在Rt△OEF中,EF=![]()
sinÐEFG= ÐEFG=arcsin
ÐEFG=arcsin![]() .(或表示为arccos
.(或表示为arccos![]() )
)
注:此题也可用空间向量的方法求解。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

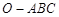 的侧棱
的侧棱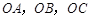 两两垂直,且
两两垂直,且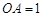 ,
,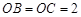 ,
,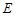 是
是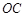 的中点。
的中点。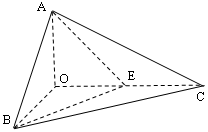
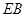 与
与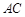 所成角的余弦值;
所成角的余弦值;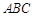 的所成角的正弦值。
的所成角的正弦值。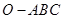 的侧棱
的侧棱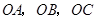 两两垂直,且
两两垂直,且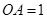 ,
,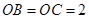 ,
,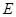 是
是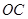 的中点.
的中点.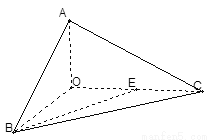
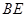 与
与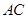 所成的角的余弦值
所成的角的余弦值 的余弦值
的余弦值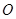 点到面
点到面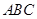 的距离
的距离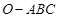 的侧棱
的侧棱 两两垂直,
两两垂直,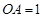 ,
,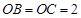 ,
, 是
是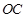 的中点。
的中点。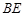 与
与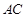 所成角的余弦值;
所成角的余弦值;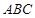 的所成角的正弦值。
的所成角的正弦值。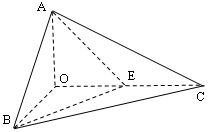
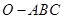 的侧棱
的侧棱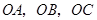 两两垂直,且
两两垂直,且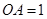 ,
,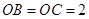 ,
,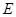 是
是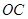 的中点.
的中点.
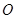 点到面
点到面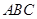 的距离;
的距离;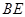 与
与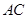 所成的角的余弦值;
所成的角的余弦值;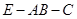 的余弦值.
的余弦值.