题目内容
已知双曲线C: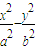 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为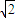 ,焦点到渐近线的距离为1.
,焦点到渐近线的距离为1.(1)求双曲线的方程;
(2)设直线y=kx+1与双曲线C的左支交于A、B两点,求k的取值范围;
(3)若另一条直线l经过点P(-2,0)及线段AB的中点,求直线l在y轴上的截距b的取值范围.
【答案】分析:(1)由双曲线C: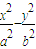 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,知a=b,由双曲线焦点(
,知a=b,由双曲线焦点( )到渐近线x±y=0的距离为1,知
)到渐近线x±y=0的距离为1,知 ,由此能求出双曲线方程.
,由此能求出双曲线方程.
(2)设A1(x1,y1),B(x2,y2),将直线y=kx+1代入双曲线x2-y2=1,得(1-k2)x2-2kx-2=0,因与左支交于两点,则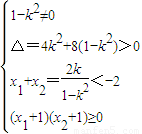 ,由此能求出k的取值范围.
,由此能求出k的取值范围.
(3)AB的中点为( ),所以直线l的方程为
),所以直线l的方程为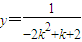 (x+2),令x=0,得b=
(x+2),令x=0,得b= =
=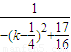 ,由此能求出b的取值范围.
,由此能求出b的取值范围.
解答:解:(1)∵双曲线C: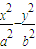 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为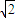 ,
,
∴a=b,
∵双曲线焦点( )到渐近线x±y=0的距离为1,
)到渐近线x±y=0的距离为1,
∴ ,
,
解得a=b=1,
∴双曲线方程为x2-y2=1.
(2)设A1(x1,y1),B(x2,y2),
将直线y=kx+1代入双曲线x2-y2=1,得
(1-k2)x2-2kx-2=0,
因与左支交于两点,则
∴
解得1<k< .
.
(3)AB的中点为(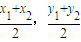 ),
),
即( ),
),
∴直线l的方程为 (x+2),
(x+2),
令x=0,得b= =
=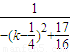 ,
,
∵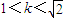 ,
,
∴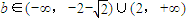 .
.
点评:本题主要考查直线与圆锥曲线的综合应用能力,综合性强,是高考的重点.本题具体涉及到轨迹方程的求法及直线与双曲线的相关知识,解题时要认真审题,注意合理地进行等价转化.
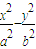 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,知a=b,由双曲线焦点(
,知a=b,由双曲线焦点( )到渐近线x±y=0的距离为1,知
)到渐近线x±y=0的距离为1,知 ,由此能求出双曲线方程.
,由此能求出双曲线方程.(2)设A1(x1,y1),B(x2,y2),将直线y=kx+1代入双曲线x2-y2=1,得(1-k2)x2-2kx-2=0,因与左支交于两点,则
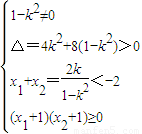 ,由此能求出k的取值范围.
,由此能求出k的取值范围.(3)AB的中点为(
 ),所以直线l的方程为
),所以直线l的方程为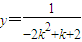 (x+2),令x=0,得b=
(x+2),令x=0,得b= =
=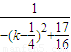 ,由此能求出b的取值范围.
,由此能求出b的取值范围.解答:解:(1)∵双曲线C:
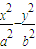 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为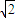 ,
,∴a=b,
∵双曲线焦点(
 )到渐近线x±y=0的距离为1,
)到渐近线x±y=0的距离为1,∴
 ,
,解得a=b=1,
∴双曲线方程为x2-y2=1.
(2)设A1(x1,y1),B(x2,y2),
将直线y=kx+1代入双曲线x2-y2=1,得
(1-k2)x2-2kx-2=0,
因与左支交于两点,则
∴

解得1<k<
 .
.(3)AB的中点为(
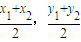 ),
),即(
 ),
),∴直线l的方程为
 (x+2),
(x+2),令x=0,得b=
 =
=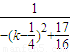 ,
,∵
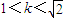 ,
,∴
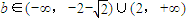 .
.点评:本题主要考查直线与圆锥曲线的综合应用能力,综合性强,是高考的重点.本题具体涉及到轨迹方程的求法及直线与双曲线的相关知识,解题时要认真审题,注意合理地进行等价转化.

练习册系列答案
相关题目
 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,右准线方程为x=
,右准线方程为x=
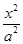 -
- =1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为(
)
=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为(
) -
-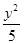 =1
B.
=1
B.  -
- =1 C.
=1 C.  -
- =1
=1 -
- =1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为
=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为 -
- =1 B、
=1 B、 -
- =1
C、
=1
C、 -
- =1[w~#
=1[w~#