题目内容
设函数f(x)=-x(x-a)2(x∈R),其中a∈R.
(1)、当f(x)奇函数时求a的值
(2)、当a=1时,求曲线y=f(x)过点(0,f(0))的切线方程;(4分)
(3)、当a≠0时,求函数f(x)的极大值和极小值;(6分)
解:(1)∵f(x)为奇函数
∴f(-x)=-f(x),
∴x(-x-a)2=x(x-a)2
∵x∈R
∴(-x-a)2=(x-a)2恒成立
∴a=0
(2)当a=1时,f(x)=-x(x-1)2=-x3+2x2-x,得f(0)=0,且f'(x)=-3x2+4x-1,
设切点(x0,-x0(x0-1)2)
所以,切线方程y+x0(x0-1)2=(-3x02+4x0-1)(x-x0)
因为(0,0)在曲线上代入求得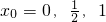
所以所求的切线方程为:y=-x;y=0;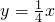 .
.
(3)f(x)=-x(x-a)2=-x3+2ax2-a2x
f'(x)=-3x2+4ax-a2=-(3x-a)(x-a).
令f'(x)=0,解得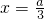 或x=a.
或x=a.
由于a≠0,以下分两种情况讨论.
(1)若a>0,当x变化时,f'(x)的正负如下表:
因此,函数f(x)在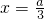 处取得极小值
处取得极小值 ,且
,且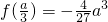 ;
;
函数f(x)在x=a处取得极大值f(a),且f(a)=0.
(2)若a<0,当x变化时,f'(x)的正负如下表:
因此,函数f(x)在x=a处取得极小值f(a),且f(a)=0;
函数f(x)在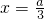 处取得极大值
处取得极大值 ,且
,且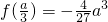 .
.
分析:(1)根据f(x)为奇函数,可得f(-x)=-f(x),代入化简可得a的值;
(2)当a=1时,f(x)=-x(x-1)2=-x3+2x2-x,得f(0)=0,且f'(x)=-3x2+4x-1,设切点(x0,-x0(x0-1)2)
可得切线方程y+x0(x0-1)2=(-3x02+4x0-1)(x-x0),将(0,0)代入,即可求得所求的切线方程;
(3)求导函数,并令f'(x)=0,解得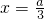 或x=a.对a分两种情况讨论,利用函数在导数为0的附近,导数的符号变化,从而确定函数f(x)的极小值与极大值.
或x=a.对a分两种情况讨论,利用函数在导数为0的附近,导数的符号变化,从而确定函数f(x)的极小值与极大值.
点评:本题以函数为载体,考查函数的性质,考查切线方程,考查函数的极值,解题的关键是利用导数的几何意义,利用导数确定函数的单调性.
∴f(-x)=-f(x),
∴x(-x-a)2=x(x-a)2
∵x∈R
∴(-x-a)2=(x-a)2恒成立
∴a=0
(2)当a=1时,f(x)=-x(x-1)2=-x3+2x2-x,得f(0)=0,且f'(x)=-3x2+4x-1,
设切点(x0,-x0(x0-1)2)
所以,切线方程y+x0(x0-1)2=(-3x02+4x0-1)(x-x0)
因为(0,0)在曲线上代入求得
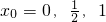
所以所求的切线方程为:y=-x;y=0;
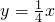 .
.(3)f(x)=-x(x-a)2=-x3+2ax2-a2x
f'(x)=-3x2+4ax-a2=-(3x-a)(x-a).
令f'(x)=0,解得
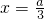 或x=a.
或x=a.由于a≠0,以下分两种情况讨论.
(1)若a>0,当x变化时,f'(x)的正负如下表:
| x | 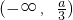 |  | 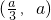 | a | (a,+∞) |
| f'(x) | - | 0 | + | 0 | - |
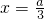 处取得极小值
处取得极小值 ,且
,且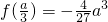 ;
;函数f(x)在x=a处取得极大值f(a),且f(a)=0.
(2)若a<0,当x变化时,f'(x)的正负如下表:
| x | (-∞,a) | a |  |  | 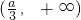 |
| f'(x) | - | 0 | + | 0 | - |
函数f(x)在
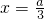 处取得极大值
处取得极大值 ,且
,且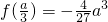 .
.分析:(1)根据f(x)为奇函数,可得f(-x)=-f(x),代入化简可得a的值;
(2)当a=1时,f(x)=-x(x-1)2=-x3+2x2-x,得f(0)=0,且f'(x)=-3x2+4x-1,设切点(x0,-x0(x0-1)2)
可得切线方程y+x0(x0-1)2=(-3x02+4x0-1)(x-x0),将(0,0)代入,即可求得所求的切线方程;
(3)求导函数,并令f'(x)=0,解得
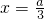 或x=a.对a分两种情况讨论,利用函数在导数为0的附近,导数的符号变化,从而确定函数f(x)的极小值与极大值.
或x=a.对a分两种情况讨论,利用函数在导数为0的附近,导数的符号变化,从而确定函数f(x)的极小值与极大值.点评:本题以函数为载体,考查函数的性质,考查切线方程,考查函数的极值,解题的关键是利用导数的几何意义,利用导数确定函数的单调性.

练习册系列答案
相关题目
设函数f(x)的定义域为A,若存在非零实数t,使得对于任意x∈C(C⊆A),有x+t∈A,且f(x+t)≤f(x),则称f(x)为C上的t低调函数.如果定义域为[0,+∞)的函数f(x)=-|x-m2|+m2,且 f(x)为[0,+∞)上的10低调函数,那么实数m的取值范围是( )
| A、[-5,5] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|