题目内容
设函数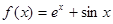 ,
,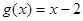 ;
;
(1)求证:函数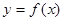 在
在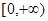 上单调递增;
上单调递增;
(2)设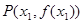 ,
,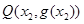
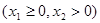 ,若直线
,若直线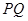
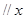 轴,求
轴,求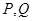 两点间的最短距离.
两点间的最短距离.
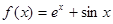 ,
,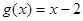 ;
;(1)求证:函数
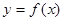 在
在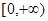 上单调递增;
上单调递增;(2)设
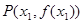 ,
,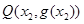
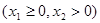 ,若直线
,若直线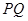
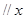 轴,求
轴,求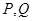 两点间的最短距离.
两点间的最短距离. (1)详见解析;(2)3.
试题分析:(1) 本小题首先利用求导的公式与法则求得函数
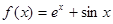 的导数,通过分析其值的正负可得函数的单调性,函数
的导数,通过分析其值的正负可得函数的单调性,函数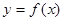 在
在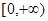 上单调递增;
上单调递增;(2) 本小题主要利用导数分析函数的单调性
 在
在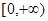 上单调递增,然后求得目标函数的最值即可。
上单调递增,然后求得目标函数的最值即可。试题解析:(1)
 时,
时, ,
,所以函数
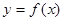 在
在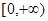 上单调递增; 6分
上单调递增; 6分(2)因为
 ,所以
,所以 8分
8分所以
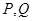 两点间的距离等于
两点间的距离等于
 , 9分
, 9分设
 ,则
,则 ,
,记
 ,则
,则 ,
,所以
 , 12分
, 12分所以
 在
在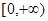 上单调递增,所以
上单调递增,所以 14分
14分所以
 ,即
,即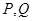 两点间的最短距离等于3. 15分
两点间的最短距离等于3. 15分
练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 满足
满足 ,
, ,设函数
,设函数
 时,求
时,求 的极小值;
的极小值; (
( )的极小值点与
)的极小值点与 的极大值小于等于
的极大值小于等于

 单调递增区间;
单调递增区间; ,使得
,使得 是自然对数的底数),求实数
是自然对数的底数),求实数 的取值范围.
的取值范围.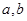 是正实数,设函数
是正实数,设函数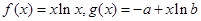 。
。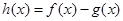 ,求
,求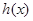 的单调区间;
的单调区间;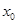 ,使
,使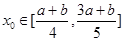 且
且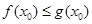 成立,求
成立,求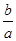 的取值范围。
的取值范围。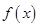 的定义域为
的定义域为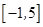 ,部分对应值如下表,
,部分对应值如下表,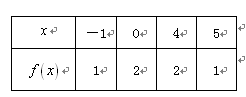
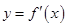 的图象如图所示.
的图象如图所示. 
 ,
,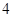 ;
;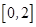 上是减函数;
上是减函数;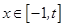 时,
时,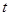 的最大值为4;
的最大值为4;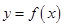 最多有2个零点.
最多有2个零点.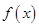 是定义在R上的可导函数,且满足
是定义在R上的可导函数,且满足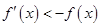 ,对于任意的正数
,对于任意的正数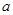 ,下面不等式恒成立的是( )
,下面不等式恒成立的是( )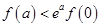
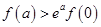

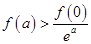
 在区间
在区间 上单调递减,则实数
上单调递减,则实数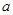 的取值范围是
的取值范围是 .
.