题目内容
设an=1+q+q2+q3+…+qn-1,An=cn1a1+cn2a2+cn3a3+…+cnnan,且-3<q<1,则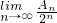 的值为
的值为
- A.

- B.
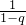
- C.q
- D.1-q
B
分析:利用等比数列的前n项和公式求出an,利用二项式系数和是2n及二项式定理的逆用,求出An.化简 ,再利用公式
,再利用公式 其中0<|q|<1求出极限值.
其中0<|q|<1求出极限值.
解答:因为q≠1,
所以an=1+q+q2+…+qn-1= .
.
于是An= Cn1+
Cn1+ Cn2+…+
Cn2+…+ Cnn
Cnn
=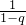 [(Cn1+Cn2+…+Cnn)-(Cn1q+Cn2q2+…+Cnnqn)]
[(Cn1+Cn2+…+Cnn)-(Cn1q+Cn2q2+…+Cnnqn)]
=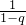 {(2n-1)-[(1+q)n-1]}
{(2n-1)-[(1+q)n-1]}
=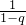 [2n-(1+q)n].
[2n-(1+q)n].
∴ =
=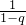 [1-(
[1-( )n].
)n].
因为-3<q<1,且q≠-1,
所以0<| |<1.
|<1.
所以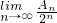 =
=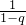 .
.
点评:本题考查等比数列的前n项和公式;二项式系数的性质;二项式定理的逆用;利用特殊的极限值求函数的极限.
分析:利用等比数列的前n项和公式求出an,利用二项式系数和是2n及二项式定理的逆用,求出An.化简
 ,再利用公式
,再利用公式 其中0<|q|<1求出极限值.
其中0<|q|<1求出极限值.解答:因为q≠1,
所以an=1+q+q2+…+qn-1=
 .
.于是An=
 Cn1+
Cn1+ Cn2+…+
Cn2+…+ Cnn
Cnn=
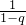 [(Cn1+Cn2+…+Cnn)-(Cn1q+Cn2q2+…+Cnnqn)]
[(Cn1+Cn2+…+Cnn)-(Cn1q+Cn2q2+…+Cnnqn)]=
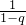 {(2n-1)-[(1+q)n-1]}
{(2n-1)-[(1+q)n-1]}=
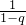 [2n-(1+q)n].
[2n-(1+q)n].∴
 =
=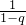 [1-(
[1-( )n].
)n].因为-3<q<1,且q≠-1,
所以0<|
 |<1.
|<1.所以
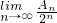 =
=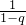 .
.点评:本题考查等比数列的前n项和公式;二项式系数的性质;二项式定理的逆用;利用特殊的极限值求函数的极限.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
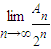 .
.