题目内容
设 、
、 是不共线的两个非零向量.
是不共线的两个非零向量.
(1)若 ,求证:
,求证: 三点共线;
三点共线;
(2)若 与
与 共线,求实数
共线,求实数 的值.
的值.
 、
、 是不共线的两个非零向量.
是不共线的两个非零向量.(1)若
 ,求证:
,求证: 三点共线;
三点共线;(2)若
 与
与 共线,求实数
共线,求实数 的值.
的值.(1)证明详见解析;(2)当 与
与 共线时,
共线时, .
.
 与
与 共线时,
共线时, .
.试题分析:(1)利用向量证明三点共线,先建立平面向量的基底
 ,求出
,求出 、
、 ,找到
,找到 使得
使得 ,从而说明
,从而说明 ,再说明两个向量有一个公共点
,再说明两个向量有一个公共点 即可;(2)根据
即可;(2)根据 与
与 共线,得到
共线,得到 ,然后根据向量相等的条件,建立
,然后根据向量相等的条件,建立 、
、 的方程组,求解即可得到
的方程组,求解即可得到 的值.
的值.试题解析:(1)证明:∵

而

∴
 与
与 共线,又有公共端点
共线,又有公共端点 ,∴
,∴ 三点共线
三点共线(2)∵
 与
与 共线,∴存在实数
共线,∴存在实数 ,使得
,使得
∵
 与
与 不共线
不共线∴
 或
或
 .
.
练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
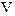 ABC所在平面内的一点,
ABC所在平面内的一点,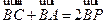 ,则( )
,则( )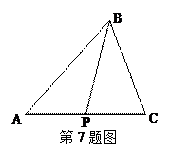





 .
.
 与
与 是不共线向量,
是不共线向量, ,若
,若 且
且 ,则实数
,则实数 的值为( )
的值为( )

 ,
, ,则
,则 在
在 上的投影的取值范围是( )
上的投影的取值范围是( )



 是已知的平面向量且
是已知的平面向量且 ,关于向量
,关于向量 ,总存在向量
,总存在向量 ,使
,使 ;
; 和
和 ,使
,使 ;
; ,且
,且 ∥
∥ ,则实数
,则实数 的值是 。
的值是 。 _________.
_________.