题目内容
△ABC的顶点B（-4，0），C（4，0），△ABC的内切圆圆心在直线x=1上，则顶点A的轨迹方程是 ．
分析：如图所示，由内切圆的性质可得：|AB|-|AC|=|BD|-|CD|=4+1-（4-1）=2＜8=|BC|，利用双曲线的定义即可判断出．
解答：解：如图所示，|AB|-|AC|=|BD|-|CD|=4+1-（4-1）=2＜8=|BC|，
因此点A在以B，C两点为焦点，1为实半轴长的双曲线x2-
=1（x＞1）上．
故答案为：x2-
=1（x＞1）．
因此点A在以B，C两点为焦点，1为实半轴长的双曲线x2-
| y2 |
| 15 |
故答案为：x2-
| y2 |
| 15 |
点评：本题考查了内切圆的性质、双曲线的定义及其标准方程，属于基础题．
练习册系列答案
相关题目
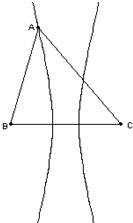如图所示的曲线是以锐角△ABC的顶点B、C为焦点，且经过点A的双曲线，若△ABC的内角的对边分别为a，b，c，且a=4，b=6，| csinA |
| a |
| ||
| 2 |
A、
| ||||
B、
| ||||
C、3-
| ||||
D、3+
|