题目内容
函数
在R上是减函数，则实数a的取值范围是________．
a≤-2
分析：由于f（x）为R上的减函数，所以当x＜-1时，恒有f（x）＞f（-1），由此可求得a的取值范围．
解答：因为f（x）为R上的减函数，所以必有f（-1）≤
，即1+a≤-1，所以a≤-2．
故答案为：-2．
点评：本题考查函数单调性的性质，数形结合法分析本题更为容易．
分析：由于f（x）为R上的减函数，所以当x＜-1时，恒有f（x）＞f（-1），由此可求得a的取值范围．
解答：因为f（x）为R上的减函数，所以必有f（-1）≤
，即1+a≤-1，所以a≤-2．故答案为：-2．
点评：本题考查函数单调性的性质，数形结合法分析本题更为容易．
练习册系列答案
相关题目
是定义在R上的偶函数，且对任意的
恒有
，
时，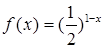
，则其中所有正确命题的序号是_____________.
上是减函数，在
上是增函数；
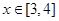时，
. 
在R上是减函数，则
的取值范围是（
）
B、
C、
D、
在
上是增函数，且具有性质：
，则该函数（
）
上是增函数
B.在
上是增函数在
上是减函数 
上是减函数 D.在
上是减函数在
上是增函数