题目内容
已知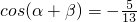
，
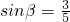，α，β均为锐角
（1）求cos（α+2β）值
（2）求sinα的值．
解：（1）由题意知：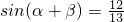
，
，
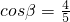∴cos（α+2β）=cos[（α+β）+β]=cos（α+β）cosβ-sin（α+β）sinβ=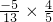
-
=-
．
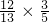（2）sinα=sin[（α+β）-β]=sin（α+β）cosβ-cos（α+β）sinβ=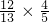
-
=
．
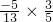分析：（1）由题意知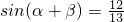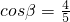：，，利用两角和的余弦公式可得 cos（α+2β）=cos[（α+β）+β]=cos（α+β）cosβ-sin（α+β）sinβ，运算求出结果．
（2）利用两角差的正弦公式可得 sinα=sin[（α+β）-β]=sin（α+β）cosβ-cos（α+β）sinβ，运算求出结果．
点评：本题主要考查两角和差的正弦、余弦公式的应用，同角三角函数的基本关系的应用，属于中档题．
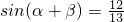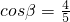，，∴cos（α+2β）=cos[（α+β）+β]=cos（α+β）cosβ-sin（α+β）sinβ=
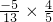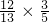-=-．（2）sinα=sin[（α+β）-β]=sin（α+β）cosβ-cos（α+β）sinβ=
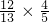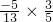-=．分析：（1）由题意知：
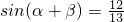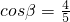，，利用两角和的余弦公式可得 cos（α+2β）=cos[（α+β）+β]=cos（α+β）cosβ-sin（α+β）sinβ，运算求出结果．（2）利用两角差的正弦公式可得 sinα=sin[（α+β）-β]=sin（α+β）cosβ-cos（α+β）sinβ，运算求出结果．
点评：本题主要考查两角和差的正弦、余弦公式的应用，同角三角函数的基本关系的应用，属于中档题．
练习册系列答案
新编小学单元自测题系列答案
字词句段篇系列答案
相关题目
的每条棱长均为
，
为棱
上的动点，
∥平面
，并证明之；
所成锐二面角的正切值。
