题目内容
等腰三角形ABC中,AB=AC=5,∠B=30°,P为BC边中线上任意一点,则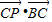 的值为( )
的值为( )A.
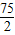
B.
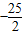
C.5
D.
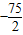
【答案】分析:以C为原点,BC所在直线为x轴,建立如图坐标系,可得向量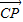 、
、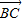 的坐标,结合平面向量数量积的坐标运算公式,即可算出
的坐标,结合平面向量数量积的坐标运算公式,即可算出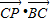 的值.
的值.
解答:解: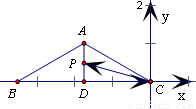 ∵等腰三角形ABC中,AB=AC=5,∠B=30°,
∵等腰三角形ABC中,AB=AC=5,∠B=30°,
∴BC=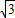 AB=5
AB=5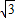 ,AD=
,AD=
以C为原点,BC所在直线为x轴,建立如图坐标系
可得B(-5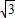 ,0),P(-
,0),P(-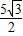 ,t),其中0<t<
,t),其中0<t<
∴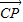 =(-
=(-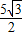 ,t),
,t),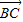 =(5
=(5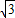 ,0)
,0)
可得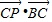 =-
=-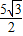 ×5
×5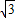 +t×0=-
+t×0=-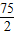
故选:D
点评:本题在底角为30度的等腰三角形中,求两个向量的数量积,着重考查了平面向量数量积的定义与坐标运算公式等知识,属于基础题.
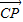 、
、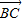 的坐标,结合平面向量数量积的坐标运算公式,即可算出
的坐标,结合平面向量数量积的坐标运算公式,即可算出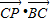 的值.
的值.解答:解:
 ∵等腰三角形ABC中,AB=AC=5,∠B=30°,
∵等腰三角形ABC中,AB=AC=5,∠B=30°,∴BC=
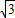 AB=5
AB=5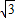 ,AD=
,AD=
以C为原点,BC所在直线为x轴,建立如图坐标系
可得B(-5
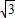 ,0),P(-
,0),P(-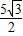 ,t),其中0<t<
,t),其中0<t<
∴
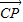 =(-
=(-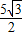 ,t),
,t),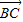 =(5
=(5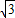 ,0)
,0)可得
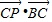 =-
=-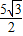 ×5
×5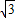 +t×0=-
+t×0=-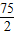
故选:D
点评:本题在底角为30度的等腰三角形中,求两个向量的数量积,着重考查了平面向量数量积的定义与坐标运算公式等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
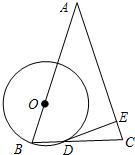 如图,在等腰三角形ABC中,AB=AC,O为AB上一点,以O为圆心、OB长为半径的圆交BC于D,DE⊥AC交AC于E.
如图,在等腰三角形ABC中,AB=AC,O为AB上一点,以O为圆心、OB长为半径的圆交BC于D,DE⊥AC交AC于E.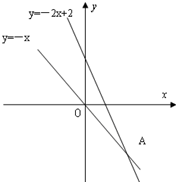 已知:等腰三角形ABC中,其中一个腰AC所在的直线方程为y=-2x+2,∠A的平分线所在的直线方程为y=-x,底边BC经过点D(-1,0),求三角形底边BC及腰AB所在的直线方程.
已知:等腰三角形ABC中,其中一个腰AC所在的直线方程为y=-2x+2,∠A的平分线所在的直线方程为y=-x,底边BC经过点D(-1,0),求三角形底边BC及腰AB所在的直线方程. (2013•徐州一模)如图,在等腰三角形ABC中,已知AB=AC=1,A=120°,E,F分别是边AB,AC上的点,且
(2013•徐州一模)如图,在等腰三角形ABC中,已知AB=AC=1,A=120°,E,F分别是边AB,AC上的点,且